Edge Detection

An edge, also known as a discontinuity, in a signal is usually defined as a transition in the intensity or amplitude of that signal. More...

Modules
	Edge Marking
	Introduction to Edge Marking
	Gradient
	Introduction to Gradient
	Laplacian
	For a 2-D function F(x,y), one might define the Laplacian operator as :
	Other Derivatives
	This group provides miscellaneous derivative based operators such as partial derivatives or Hessian Matrix.

Detailed Description

An edge, also known as a discontinuity, in a signal is usually defined as a transition in the intensity or amplitude of that signal.

Edge detection is based upon the detection of local discontinuities which mainly correspond to the boundaries of objects in an image.

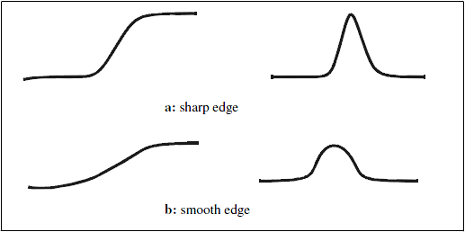
Typically, an ideal one-dimensional edge can be defined as a step from low to high intensity, as in Figure 1. In practice, the signal is usually corrupted by noise. In which case, the edge is defined as the transition from an average low to an average high intensity. Such edges are characterized by their contrast (difference between high and low intensity), and their width or rate-of-change. These measures differentiate between sharp and smooth edges.

Figure 1: 1-D edge model

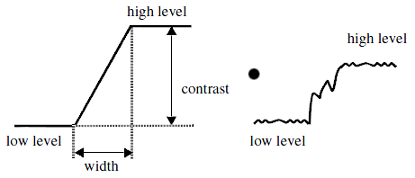
In two dimensions, the discontinuities occur along certain lines or orientations. Figure 2 depicts a 2-D step or ramp edge. As in the 1-D case, a width or rate-of change, and a contrast can be defined. In addition, the local orientation feature is important in characterizing 2-D edges.

Figure 2: 2-D step edge

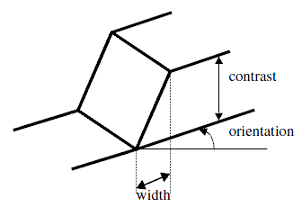
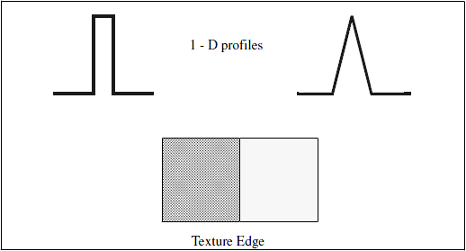
Note that this model is not unique, and that other definitions exist using the transition profile or the color and texture properties. Some examples of these edges are shown in the Figure 3, although their presentation is beyond the scope of this manual, where we primarily investigate luminance edges.

Figure 3: Other edge models

In the 1-D case (Figure 4-a), the transition point can be marked as the maximum of the first-order derivative (Figure 4-b), or the zero-crossing of the second-order derivative (Figure 4-c).

Figure 4: 1-D function and its derivatives

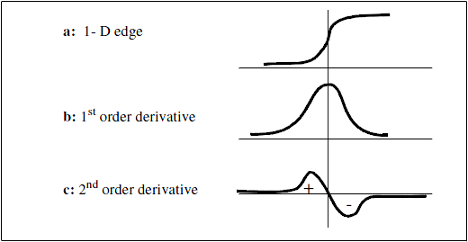
Notice that the first-order derivative is higher for a sharp transition profile than for a smooth transition as shown in Figure 5.

Figure 5: Sharp and smooth edges

These facts suggest a strategy for edge detection:

• Enhance local edges using differentiation,
• Threshold the result so that only the points of a sufficiently large derivative are retained as edge points.

The extension of such 1st- and 2nd-order derivatives to the 2-D case are based upon the use of the Gradient and Laplacian, respectively.