Open Inventor Mentor, 2nd Edition - Volume I > Curves and Surfaces > NURBS Surfaces

20.4. NURBS Surfaces

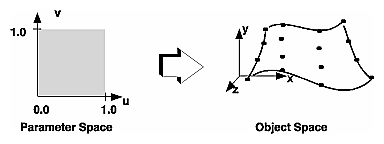
A surface differs from a curve only in that it has two parametric directions (u and v) instead of one (Figure 20.14, “ Curved Surfaces ”), and that the order and knot vector must be specified for both parameters.

Curved Surfaces

Figure 20.14.  Curved Surfaces


The two parametric dimensions, u and v, are mapped to 3D object space. As with curves, control points are specified in object space. The u and v parameters can have a different order, and a different knot sequence, although they are often the same. The order for each dimension is specified as

order = number_of_knots - number_of_control_points

[Tip]

Tip: Put NURBS shapes under their own separator to facilitate caching.

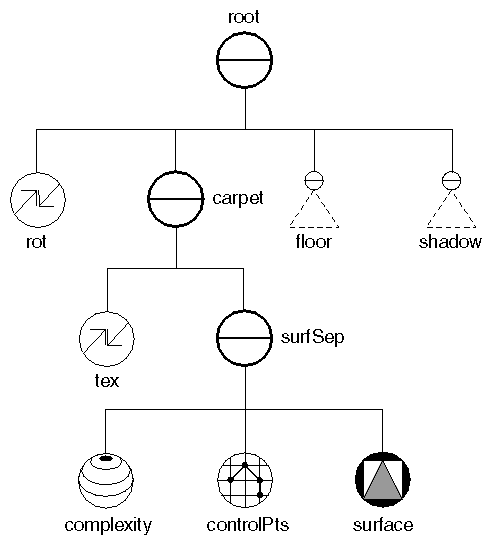
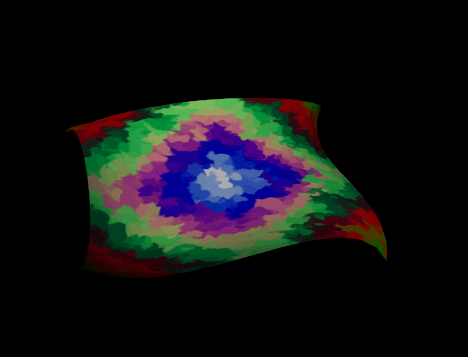
Bezier Surface

Example 20.3, “ Bezier Surface ” creates a plain Bezier surface. The knot vectors define a cubic Bezier surface (multiplicity 4 at beginning and end). The surface is order 4 with 16 control points arranged in a four-by-four grid. The u and v knot vectors each have a length of 8. Figure 20.15, “ Scene Graph for a Bezier Surface ” shows the scene graph for the nodes in this example. Notice that the points used as control points (controlPts) must precede the NURBS node (surface) in the scene graph. Figure 20.16, “ Bezier Surface” shows the rendered image.

Scene Graph for a Bezier Surface

Figure 20.15.  Scene Graph for a Bezier Surface


Bezier Surface

Figure 20.16.  Bezier Surface


Example 20.3.  Bezier Surface

C++
// The control points for this surface
float pts[16][3] =
{
   {-4.5, -2.0,  8.0},
   {-2.0,  1.0,  8.0},
   { 2.0, -3.0,  6.0},
   { 5.0, -1.0,  8.0},
   {-3.0,  3.0,  4.0},
   { 0.0, -1.0,  4.0},
   { 1.0, -1.0,  4.0},
   { 3.0,  2.0,  4.0},
   {-5.0, -2.0, -2.0},
   {-2.0, -4.0, -2.0},
   { 2.0, -1.0, -2.0},
   { 5.0,  0.0, -2.0},
   {-4.5,  2.0, -6.0},
   {-2.0, -4.0, -5.0},
   { 2.0,  3.0, -5.0},
   { 4.5, -2.0, -6.0}
};

// The knot vector
float knots[8] =
{
   0, 0, 0, 0, 1, 1, 1, 1
};

// Create the nodes needed for the Bezier surface.
SoSeparator *
makeSurface()
{
 SoSeparator *surfSep = new SoSeparator();
 surfSep->ref();

 // Define the Bezier surface including the control
 // points and a complexity.
 SoComplexity  *complexity = new SoComplexity;
 SoCoordinate3 *controlPts = new SoCoordinate3;
 SoNurbsSurface  *surface  = new SoNurbsSurface;
 complexity->value = 0.7;
 controlPts->point.setValues(0, 16, pts);
 surface->numUControlPoints = 4;
 surface->numVControlPoints = 4;
 surface->uKnotVector.setValues(0, 8, knots);
 surface->vKnotVector.setValues(0, 8, knots);
 surfSep->addChild(complexity);
 surfSep->addChild(controlPts);
 surfSep->addChild(surface);

 surfSep->unrefNoDelete();
 return surfSep;
}
.NET
// The control points for this surface
float[,] pts = new float[16, 3] 
{
  {-4.5f, -2.0f,  8.0f},
  {-2.0f,  1.0f,  8.0f},
  { 2.0f, -3.0f,  6.0f},
  { 5.0f, -1.0f,  8.0f},
  {-3.0f,  3.0f,  4.0f},
  { 0.0f, -1.0f,  4.0f},
  { 1.0f, -1.0f,  4.0f},
  { 3.0f,  2.0f,  4.0f},
  {-5.0f, -2.0f, -2.0f},
  {-2.0f, -4.0f, -2.0f},
  { 2.0f, -1.0f, -2.0f},
  { 5.0f,  0.0f, -2.0f},
  {-4.5f,  2.0f, -6.0f},
  {-2.0f, -4.0f, -5.0f},
  { 2.0f,  3.0f, -5.0f},
  { 4.5f, -2.0f, -6.0f}
};

// The knot vector
float[] knots = new float[8]
{
  0, 0, 0, 0, 
  1, 1, 1, 1
};

// Create the nodes needed for the Bezier surface.
SoSeparator
MakeSurface()
{
  SoSeparator surfSep = new SoSeparator();

  // Define the Bezier surface including the control
  // points and a complexity.
  SoComplexity complexity = new SoComplexity();
  SoCoordinate3 controlPts = new SoCoordinate3();
  SoNurbsSurface surface = new SoNurbsSurface();
  complexity.value.Value = 0.7f;
  controlPts.point.SetValues(0, 16, pts);
  surface.numUControlPoints.Value = 4;
  surface.numVControlPoints.Value = 4;
  surface.uKnotVector.SetValues(0, knots);
  surface.vKnotVector.SetValues(0, knots);
  surfSep.AddChild(complexity);
  surfSep.AddChild(controlPts);
  surfSep.AddChild(surface);

  return surfSep;
}
Java
//The control points for this surface
float[][] pts = new float[][]
{
    {-4.5f, -2.0f,  8.0f},
    {-2.0f,  1.0f,  8.0f},
    { 2.0f, -3.0f,  6.0f},
    { 5.0f, -1.0f,  8.0f},
    {-3.0f,  3.0f,  4.0f},
    { 0.0f, -1.0f,  4.0f},
    { 1.0f, -1.0f,  4.0f},
    { 3.0f,  2.0f,  4.0f},
    {-5.0f, -2.0f, -2.0f},
    {-2.0f, -4.0f, -2.0f},
    { 2.0f, -1.0f, -2.0f},
    { 5.0f,  0.0f, -2.0f},
    {-4.5f,  2.0f, -6.0f},
    {-2.0f, -4.0f, -5.0f},
    { 2.0f,  3.0f, -5.0f},
    { 4.5f, -2.0f, -6.0f}
};

// The knot vector
float[] knots = new float[]
{
    0, 0, 0, 0, 
    1, 1, 1, 1
};

// Create the nodes needed for the Bezier surface.
SoSeparator
makeSurface()
{
  SoSeparator surfSep = new SoSeparator();

  // Define the Bezier surface including the control
  // points and a complexity.
  SoComplexity complexity = new SoComplexity();
  SoCoordinate3 controlPts = new SoCoordinate3();
  SoNurbsSurface surface = new SoNurbsSurface();
  complexity.value.setValue(0.7f);
  controlPts.point.setValues(0, pts);
  surface.numUControlPoints.setValue(4);
  surface.numVControlPoints.setValue(4);
  surface.uKnotVector.setValues(0, knots);
  surface.vKnotVector.setValues(0, knots);
  surfSep.addChild(complexity);
  surfSep.addChild(controlPts);
  surfSep.addChild(surface);

  return surfSep;
}

[Tip]

Tip: If a NURBS surface is changing, inserting an SoComplexity( C++ | Java | .NET ) node with SCREEN_SPACE specified as the type may improve performance, especially if the NURBS surfaces are far away.

Trimming NURBS Surfaces

Profile curves are used to trim (cut areas away from) a NURBS surface. Profile curves themselves are not rendered; they are simply used to trim any subsequent NURBS surfaces in the scene graph. Like transformations, profile curves are pushed and popped by separator groups, yet they accumulate with each other.

Profile curves are often used to perform a stencil operation, such as cutting a shape out of a cloth surface with a pair of scissors. They are also used to remove sharp corners from a NURBS surface. See also Example 6-3, which uses a profile curve with 3D text.

Trimming NURBS surfaces is considered an advanced topic. If this is your first exposure to a NURBS, experiment first with curves and surfaces, then move on to trimmed surfaces.

A profile curve can consist of a linear profile curve (SoLinearProfile( C++ | Java | .NET )), a NURBS curve (SoNurbsProfileCurve), or a combination of the two. For coordinates, it uses either SoProfileCoordinate2( C++ | Java | .NET ) (for nonrational profile curves) orSoProfileCoordinate3( C++ | Java | .NET ) (for rational profile curves). The main requirement is that the composite profile curve make a complete loop, with its first point repeated as its last point. In addition, it cannot be self-intersecting.

[Tip]

Tip: If you want your profile curve to be straight but follow the surface, use an SoNurbsProfileCurve with an order 2 curve. (See Example 20.4, “ Trimming a Bezier Surface ”.) Linear profiles create straight trim edges in object space that do not follow the surface. You will seldom use an SoLinearProfile( C++ | Java | .NET ) to trim a NURBS surface.

The direction in which the points of a profile curve are defined is significant. If the profile curve is defined in a clockwise direction, the area inside the curve is discarded and the area outside the curve is retained. If the profile curve is defined in a counterclockwise direction, the area inside is retained and the area outside is discarded. Profile curves can be nested inside each other but cannot intersect each other. The outermost profile curve must be defined in a counterclockwise direction (see Example 20.4, “ Trimming a Bezier Surface ”).

Profile curves are defined in parameter space, which is mapped to object space.

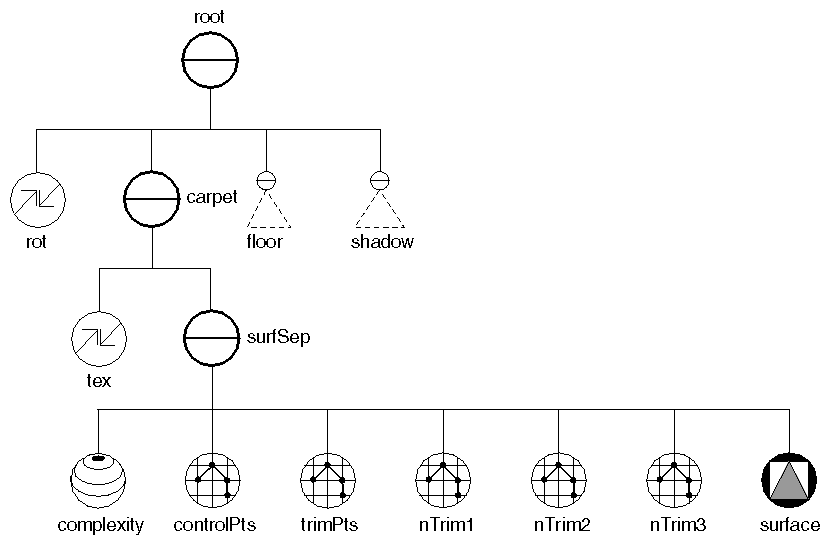
Example 20.4, “ Trimming a Bezier Surface ” adds profile curves to the surface created in Example 20.3, “ Bezier Surface ”. Figure 20.17, “ Scene Graph for Trimmed Bezier Surface ” shows the scene graph for the nodes in this example. Notice that the points used as control points (controlPts) must precede the NURBS node (surface) in the scene graph. Similarly, the points that define the profile curve (trimPts) must precede the profile-curve nodes (nTrim1, nTrim2, and nTrim3). And, naturally, the profile-curve nodes must precede the NURBS surface to be trimmed.

Scene Graph for Trimmed Bezier Surface

Figure 20.17.  Scene Graph for Trimmed Bezier Surface


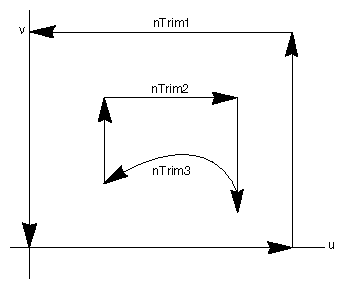
Figure 20.18, “ Trim Curves Used in Example 8-4 ” shows the trim curves used in Example 20.4, “ Trimming a Bezier Surface ”, mapped in parameter (u/v) space. This example uses three NURBS profile curves. Each curve has its own knot vector. The first curve, nTrim1, has four segments and five control points (it starts and ends at the same point). It is an order 2 curve that passes through the endpoints. The second profile curve, nTrim2, is also linear. It passes through the endpoints and has three segments. The third profile curve, nTrim3, is a cubic curve (order = 4). It has a multiplicity 4 at beginning and end (which makes it a Bezier curve that passes through the endpoints).

Notice that these trim curves are nested inside each other and that the outermost curve is counterclockwise. They do not intersect each other. Figure 20.19, “ A Trimmed Bezier Surface” shows the trimmed Bezier surface produced by Example 20.4, “ Trimming a Bezier Surface ”.

Trim Curves Used in Example 8-4

Figure 20.18.  Trim Curves Used in Example 8-4


A Trimmed Bezier Surface

Figure 20.19.  A Trimmed Bezier Surface


Example 20.4.  Trimming a Bezier Surface

C++
// The array of trim coordinates
float tpts[12][2] = {
   {0.0, 0.0},
   {1.0, 0.0},
   {1.0, 1.0},
   {0.0, 1.0},
   {0.2, 0.2},
   {0.2, 0.7},
   {0.9, 0.7},
   {0.9, 0.2},
   {0.7, 0.0},
   {0.4, 0.8}};

// The 16 coordinates defining the Bezier surface. 
float pts[16][3] = {
   {-4.5, -2.0,  8.0},
   {-2.0,  1.0,  8.0},
   { 2.0, -3.0,  6.0},
   { 5.0, -1.0,  8.0},
   {-3.0,  3.0,  4.0},
   { 0.0, -1.0,  4.0},
   { 1.0, -1.0,  4.0},
   { 3.0,  2.0,  4.0},
   {-5.0, -2.0, -2.0},
   {-2.0, -4.0, -2.0},
   { 2.0, -1.0, -2.0},
   { 5.0,  0.0, -2.0},
   {-4.5,  2.0, -6.0},
   {-2.0, -4.0, -5.0},
   { 2.0,  3.0, -5.0},
   { 4.5, -2.0, -6.0}};

// The 3 knot vectors for the 3 trim curves.
float tknots1[7] = {0, 0, 1, 2, 3, 4, 4};
float tknots2[6] = {0, 0, 1, 2, 3, 3};
float tknots3[8] = {0, 0, 0, 0, 1, 1, 1, 1};

// The Bezier knot vector for the surface.
// This knot vector is used in both the U and
// V directions.
float knots[8] = {0, 0, 0, 0, 1, 1, 1, 1};

// Create the nodes needed for the Bezier patch
// and its trim curves.
SoSeparator *
makeSurface()
{
  SoSeparator *surfSep = new SoSeparator();
  surfSep->ref();
  
  // Define the Bezier surface including the control
  // points, trim curve, and a complexity.
  SoComplexity  *complexity     = new SoComplexity;
  SoCoordinate3 *controlPts     = new SoCoordinate3;
  SoNurbsSurface *surface       = new SoNurbsSurface;
  complexity->value = 0.7;
  controlPts->point.setValues(0, 16, pts);
  surface->numUControlPoints.setValue(4);
  surface->numVControlPoints.setValue(4);
  surface->uKnotVector.setValues(0, 8, knots);
  surface->vKnotVector.setValues(0, 8, knots);
  surfSep->addChild(complexity);
  surfSep->addChild(controlPts);
  
  SoProfileCoordinate2 *trimPts = new SoProfileCoordinate2;
  SoNurbsProfile *nTrim1        = new SoNurbsProfile;
  SoNurbsProfile *nTrim2        = new SoNurbsProfile;
  SoNurbsProfile *nTrim3        = new SoNurbsProfile;
  long trimInds[5];
  
  trimPts->point.setValues(0, 12, tpts);
  trimInds[0] = 0;
  trimInds[1] = 1;
  trimInds[2] = 2;
  trimInds[3] = 3;
  trimInds[4] = 0;
  nTrim1->index.setValues(0, 5, trimInds);
  nTrim1->knotVector.setValues(0, 7, tknots1);
  trimInds[0] = 4;
  trimInds[1] = 5;
  trimInds[2] = 6;
  trimInds[3] = 7;
  nTrim2->linkage.setValue(SoProfile::START_NEW);
  nTrim2->index.setValues(0, 4, trimInds);
  nTrim2->knotVector.setValues(0, 6, tknots2);
  trimInds[0] = 7;
  trimInds[1] = 8;
  trimInds[2] = 9;
  trimInds[3] = 4;
  nTrim3->linkage.setValue(SoProfile::ADD_TO_CURRENT);
  nTrim3->index.setValues(0, 4, trimInds);
  nTrim3->knotVector.setValues(0, 8, tknots3);
  
  surfSep->addChild(trimPts);
  surfSep->addChild(nTrim1);
  surfSep->addChild(nTrim2);
  surfSep->addChild(nTrim3);
  surfSep->addChild(surface);
  
  surfSep->unrefNoDelete();
  return surfSep;
}
.NET
// The array of trim coordinates 
float[,] tpts = new float[10, 2] 
{
  { 0.0f, 0.0f },
  { 1.0f, 0.0f },
  { 1.0f, 1.0f },
  { 0.0f, 1.0f },
  { 0.2f, 0.2f },
  { 0.2f, 0.7f },
  { 0.9f, 0.7f },
  { 0.9f, 0.2f },
  { 0.7f, 0.0f },
  { 0.4f, 0.8f }
};

// The 16 coordinates defining the Bezier surface. 
float[,] pts = new float[16, 3]
{
  {-4.5f,-2.0f, 8.0f},
  {-2.0f, 1.0f, 8.0f},
  { 2.0f,-3.0f, 6.0f},
  { 5.0f,-1.0f, 8.0f},
  {-3.0f, 3.0f, 4.0f},
  { 0.0f,-1.0f, 4.0f},
  { 1.0f,-1.0f, 4.0f},
  { 3.0f, 2.0f, 4.0f},
  {-5.0f,-2.0f,-2.0f},
  {-2.0f,-4.0f,-2.0f},
  { 2.0f,-1.0f,-2.0f},
  { 5.0f, 0.0f,-2.0f},
  {-4.5f, 2.0f,-6.0f},
  {-2.0f,-4.0f,-5.0f},
  { 2.0f, 3.0f,-5.0f},
  { 4.5f,-2.0f,-6.0f}
};

// The 3 knot vectors for the 3 trim curves.
float[] tknots1 = new float[7] { 0.0f, 0.0f, 1.0f, 2.0f, 3.0f, 4.0f, 4.0f };
float[] tknots2 = new float[6] { 0.0f, 0.0f, 1.0f, 2.0f, 3.0f, 3.0f };
float[] tknots3 = new float[8] { 0.0f, 0.0f, 0.0f, 0.0f, 1.0f, 1.0f, 1.0f, 1.0f };

// The Bezier knot vector for the surface.
// This knot vector is used in both the U and
// V directions.
float[] knots = new float[8] { 0.0f, 0.0f, 0.0f, 0.0f, 1.0f, 1.0f, 1.0f, 1.0f };

// Create the nodes needed for the Bezier patch
// and its trim curves.
SoSeparator MakeSurface()
{
  SoSeparator surfSep = new SoSeparator();

  // Define the Bezier surface including the control
  // points, trim curve, and a complexity.
  SoComplexity complexity = new SoComplexity();
  SoCoordinate3 controlPts = new SoCoordinate3();
  SoNurbsSurface surface = new SoNurbsSurface();
  complexity.value.Value = 0.7f;
  controlPts.point.SetValues(0, 16, pts);
  surface.numUControlPoints.Value = 4;
  surface.numVControlPoints.Value = 4;
  surface.uKnotVector.SetValues(0, knots);
  surface.vKnotVector.SetValues(0, knots);
  surfSep.AddChild(complexity);
  surfSep.AddChild(controlPts);

  SoProfileCoordinate2 trimPts = new SoProfileCoordinate2();
  SoNurbsProfile nTrim1 = new SoNurbsProfile();
  SoNurbsProfile nTrim2 = new SoNurbsProfile();
  SoNurbsProfile nTrim3 = new SoNurbsProfile();
  Int32[] trimInds = new Int32[5];

  trimPts.point.SetValues(0, 12, tpts);
  trimInds[0] = 0;
  trimInds[1] = 1;
  trimInds[2] = 2;
  trimInds[3] = 3;
  trimInds[4] = 0;
  nTrim1.index.SetValues(0, trimInds);
  nTrim1.knotVector.SetValues(0, tknots1);
  trimInds[0] = 4;
  trimInds[1] = 5;
  trimInds[2] = 6;
  trimInds[3] = 7;
  nTrim2.linkage.Value = SoProfile.Profiles.START_NEW;
  nTrim2.index.SetValues(0, trimInds);
  nTrim2.knotVector.SetValues(0, tknots2);
  trimInds[0] = 7;
  trimInds[1] = 8;
  trimInds[2] = 9;
  trimInds[3] = 4;
  nTrim3.linkage.Value = SoProfile.Profiles.ADD_TO_CURRENT;
  nTrim3.index.SetValues(0, trimInds);
  nTrim3.knotVector.SetValues(0, tknots3);

  surfSep.AddChild(trimPts);
  surfSep.AddChild(nTrim1);
  surfSep.AddChild(nTrim2);
  surfSep.AddChild(nTrim3);
  surfSep.AddChild(surface);

  return surfSep;
}
Java
//The array of trim coordinates 
float[][] tpts = new float[][]
{
    { 0.0f, 0.0f },
    { 1.0f, 0.0f },
    { 1.0f, 1.0f },
    { 0.0f, 1.0f },
    { 0.2f, 0.2f },
    { 0.2f, 0.7f },
    { 0.9f, 0.7f },
    { 0.9f, 0.2f },
    { 0.7f, 0.0f },
    { 0.4f, 0.8f }
};

// The 16 coordinates defining the Bezier surface. 
float[][] pts = new float[][]
{
    {-4.5f,-2.0f, 8.0f},
    {-2.0f, 1.0f, 8.0f},
    { 2.0f,-3.0f, 6.0f},
    { 5.0f,-1.0f, 8.0f},
    {-3.0f, 3.0f, 4.0f},
    { 0.0f,-1.0f, 4.0f},
    { 1.0f,-1.0f, 4.0f},
    { 3.0f, 2.0f, 4.0f},
    {-5.0f,-2.0f,-2.0f},
    {-2.0f,-4.0f,-2.0f},
    { 2.0f,-1.0f,-2.0f},
    { 5.0f, 0.0f,-2.0f},
    {-4.5f, 2.0f,-6.0f},
    {-2.0f,-4.0f,-5.0f},
    { 2.0f, 3.0f,-5.0f},
    { 4.5f,-2.0f,-6.0f}
};

// The 3 knot vectors for the 3 trim curves.
float[] tknots1 = new float[] { 0.0f, 0.0f, 1.0f, 2.0f, 3.0f, 4.0f, 4.0f };
float[] tknots2 = new float[] { 0.0f, 0.0f, 1.0f, 2.0f, 3.0f, 3.0f };
float[] tknots3 = new float[] { 0.0f, 0.0f, 0.0f, 0.0f, 1.0f, 1.0f, 1.0f, 1.0f };

// The Bezier knot vector for the surface.
// This knot vector is used in both the U and
// V directions.
float[] knots = new float[] { 0.0f, 0.0f, 0.0f, 0.0f, 1.0f, 1.0f, 1.0f, 1.0f };

// Create the nodes needed for the Bezier patch
// and its trim curves.
SoSeparator MakeSurface()
{
  SoSeparator surfSep = new SoSeparator();

  // Define the Bezier surface including the control
  // points, trim curve, and a complexity.
  SoComplexity complexity = new SoComplexity();
  SoCoordinate3 controlPts = new SoCoordinate3();
  SoNurbsSurface surface = new SoNurbsSurface();
  complexity.value.setValue(0.7f);
  controlPts.point.setValues(0, pts);
  surface.numUControlPoints.setValue(4);
  surface.numVControlPoints.setValue(4);
  surface.uKnotVector.setValues(0, knots);
  surface.vKnotVector.setValues(0, knots);
  surfSep.addChild(complexity);
  surfSep.addChild(controlPts);

  SoProfileCoordinate2 trimPts = new SoProfileCoordinate2();
  SoNurbsProfile nTrim1 = new SoNurbsProfile();
  SoNurbsProfile nTrim2 = new SoNurbsProfile();
  SoNurbsProfile nTrim3 = new SoNurbsProfile();
  int[] trimInds = new int[5];

  trimPts.point.setValues(0, tpts);
  trimInds[0] = 0;
  trimInds[1] = 1;
  trimInds[2] = 2;
  trimInds[3] = 3;
  trimInds[4] = 0;
  nTrim1.index.setValues(0, trimInds);
  nTrim1.knotVector.setValues(0, tknots1);
  trimInds[0] = 4;
  trimInds[1] = 5;
  trimInds[2] = 6;
  trimInds[3] = 7;
  nTrim2.linkage.setValue(SoProfile.Profiles.START_NEW);
  nTrim2.index.setValues(0, trimInds);
  nTrim2.knotVector.setValues(0, tknots2);
  trimInds[0] = 7;
  trimInds[1] = 8;
  trimInds[2] = 9;
  trimInds[3] = 4;
  nTrim3.linkage.setValue(SoProfile.Profiles.ADD_TO_CURRENT);
  nTrim3.index.setValues(0, trimInds);
  nTrim3.knotVector.setValues(0, tknots3);

  surfSep.addChild(trimPts);
  surfSep.addChild(nTrim1);
  surfSep.addChild(nTrim2);
  surfSep.addChild(nTrim3);
  surfSep.addChild(surface);

  return surfSep;
}

Prev Up Next
20.3. Examples of NURBS Curves Home 20.5. Suggestions for Further Reading