A node kit contains a collection of nodes. The node kit manages these nodes and how they are arranged in its subgraph. You can create and remove these nodes, or parts, of the node kit. But, because the node kit is actually managing these parts, you do not have direct access to them. These parts are referred to as the hidden children of the node kit. Although a node kit is a grouping of nodes, it is not subclassed from SoGroup( C++ | Java | .NET ); methods such as addChild() do not exist for node kits.
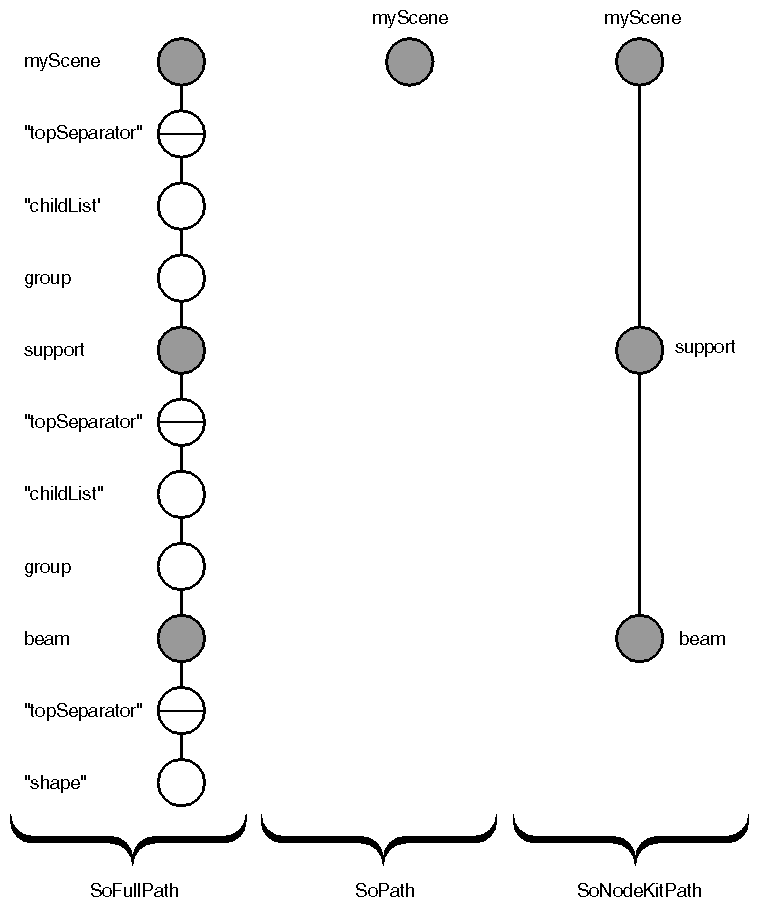
Whenever you perform a pick or a search action, a path may be returned. The default path returned, SoPath( C++ | Java | .NET ), stops at the first node in the path that has hidden children (often a node kit). If you need more detailed information about what is in the path underneath the node kit, you can cast the SoPath( C++ | Java | .NET ) to an SoFullPath, which includes hidden children as well as public children. If, for example, you search for spheres in a given scene graph, you may get a path to a node kit with hidden children, one of which is a sphere. The SoPath( C++ | Java | .NET ) returned by the search action ends in the node kit. In most cases, you can probably ignore the hidden children. But if you need information about them, you can cast this path to an SoFullPath.
You will probably use node kit paths more often than you use full paths. If you use full paths with node kits, take care not to change the node kit's structure.
![[Tip]](../images/tip.jpg) | |
Tip: When you cast a path (not a pointer) to a full path, be sure to cast a pointer; otherwise a new instance of the path is created. For example, you can do this: C++ SoPath &pathRef; ((SoFullPath *) &pathRef)->getLength(); But don't do this: length = ((SoFullPath) pathRef).getLength(); |
Another kind of path is the SoNodeKitPath( C++ | Java | .NET ), which contains only the node kits and leaves out the intermediate nodes in the path. You might use a node-kit path if you are looking at a motion hierarchy (see Example 16.3, “ Using Node Kits to Create a Motion Hierarchy ”) and you want to think of each kit as an object. Figure 16.1, “ Different Types of Paths ” shows a path, a full path, and a node-kit path for the same subgraph. The shaded circles are node kits, and the light circles are not.