By convention, all inputs and outputs for the arithmetic engines in Inventor are multiple-value (MF) fields. If you supply a value of type SoSF, it is automatically converted to an MF field. Another important feature is that if you supply an array of values for one of the inputs, the output will also be an array (an MF value). If an engine has more than one input, some inputs may have more values than others. For example, input1 might have five values and input2 might have only three values. In such cases, the last value of the field with fewer values is repeated as necessary to fill out the array. (Here, the third value of input2 would be repeated two more times.)
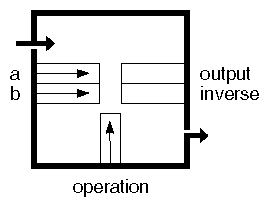
As shown in Figure 15.14, “ SoBoolOperation Engine ”, the Boolean engine, SoBoolOperation SoBoolOperation SoBoolOperation , has two Boolean inputs (a and b) and one SoSFEnum SoSFEnum input (operation) that describes the operation to be performed.
The value for operation can be one of the following:
|
Operation |
Output Is TRUE If |
|---|---|
|
CLEA R |
never TRUE |
|
SET |
always TRUE |
|
A |
A is TRUE |
|
NOT_A |
A is FALSE |
|
B |
B is TRUE |
|
NOT_B |
B is FALSE |
|
A_OR_B |
A is TRUE or B is TRUE |
|
NOT_A_OR_B |
A is FALSE or B is TRUE |
|
A_OR_NOT_B |
A is TRUE or B is FALSE |
|
NOT_A_OR_NOT_B |
A is FALSE or B is FALSE |
|
A_AND_B |
A and B are TRUE |
|
NOT_A_AND_B |
A is FALSE and B is TRUE |
|
A_AND_NOT_B |
A is TRUE and B is FALSE |
|
NOT_A_AND_NOT_B |
A and B are FALSE |
|
A_EQUALS_B |
A equals B |
|
A_NOT_EQUALS_B |
A does not equal B |
This engine has two outputs, output and inverse. The inverse field is TRUE if output is FALSE, and vice versa. If either of the inputs contains an array of values (they are of type SoMFBool SoMFBool SoMFBool ), the output will also contain an array of values.
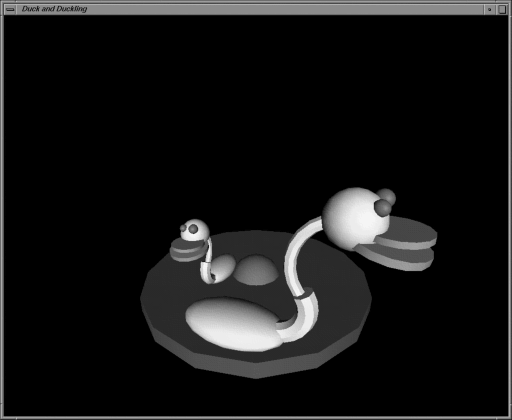
Example 15.5, “ Using a Boolean Engine ” modifies Example 15.4, “ Using a Gate Engine ” and adds a Boolean engine to make the motion of the smaller duck depend on the motion of the larger duck. The smaller duck moves when the larger duck is still. Figure 15.15, “ Swimming Ducks Controlled by a Boolean Engine ” shows an image created by this example.
Example 15.5. Using a Boolean Engine
// Bigger duck group SoSeparator *bigDuck = new SoSeparator; root->addChild(bigDuck); SoRotationXYZ *bigDuckRotXYZ = new SoRotationXYZ; bigDuck->addChild(bigDuckRotXYZ); SoTransform *bigInitialTransform = new SoTransform; bigInitialTransform->translation.setValue(0., 0., 3.5); bigInitialTransform->scaleFactor.setValue(6., 6., 6.); bigDuck->addChild(bigInitialTransform); bigDuck->addChild(duckObject); // Smaller duck group SoSeparator *smallDuck = new SoSeparator; root->addChild(smallDuck); SoRotationXYZ *smallDuckRotXYZ = new SoRotationXYZ; smallDuck->addChild(smallDuckRotXYZ); SoTransform *smallInitialTransform = new SoTransform; smallInitialTransform->translation.setValue(0., -2.24, 1.5); smallInitialTransform->scaleFactor.setValue(4., 4., 4.); smallDuck->addChild(smallInitialTransform); smallDuck->addChild(duckObject); // Use a gate engine to start/stop the rotation of // the bigger duck. SoGate *bigDuckGate = new SoGate(SoMFFloat::getClassTypeId()); SoElapsedTime *bigDuckTime = new SoElapsedTime; bigDuckGate->input->connectFrom(&bigDuckTime->timeOut); bigDuckRotXYZ->axis = SoRotationXYZ::Y; bigDuckRotXYZ->angle.connectFrom(bigDuckGate->output); // Each mouse button press will enable/disable the gate // controlling the bigger duck. SoEventCallback *myEventCB = new SoEventCallback; myEventCB->addEventCallback( SoMouseButtonEvent::getClassTypeId(), myMousePressCB, bigDuckGate); root->addChild(myEventCB); // Use a Boolean engine to make the rotation of the smaller // duck depend on the bigger duck. The smaller duck moves // only when the bigger duck is still. SoBoolOperation *myBoolean = new SoBoolOperation; myBoolean->a.connectFrom(&bigDuckGate->enable); myBoolean->operation = SoBoolOperation::NOT_A; SoGate *smallDuckGate = new SoGate(SoMFFloat::getClassTypeId()); SoElapsedTime *smallDuckTime = new SoElapsedTime; smallDuckGate->input->connectFrom(&smallDuckTime->timeOut); smallDuckGate->enable.connectFrom(&myBoolean->output); smallDuckRotXYZ->axis = SoRotationXYZ::Y; smallDuckRotXYZ->angle.connectFrom(smallDuckGate->output);
// Bigger duck group SoSeparator bigDuck = new SoSeparator(); root.AddChild(bigDuck); SoRotationXYZ bigDuckRotXYZ = new SoRotationXYZ(); bigDuck.AddChild(bigDuckRotXYZ); SoTransform bigInitialTransform = new SoTransform(); bigInitialTransform.translation.SetValue(0.0f, 0.0f, 3.5f); bigInitialTransform.scaleFactor.SetValue(6.0f, 6.0f, 6.0f); bigDuck.AddChild(bigInitialTransform); bigDuck.AddChild(duckObject); // Smaller duck group SoSeparator smallDuck = new SoSeparator(); root.AddChild(smallDuck); SoRotationXYZ smallDuckRotXYZ = new SoRotationXYZ(); smallDuck.AddChild(smallDuckRotXYZ); SoTransform smallInitialTransform = new SoTransform(); smallInitialTransform.translation.SetValue(0.0f, -2.24f, 1.5f); smallInitialTransform.scaleFactor.SetValue(4.0f, 4.0f, 4.0f); smallDuck.AddChild(smallInitialTransform); smallDuck.AddChild(duckObject); // Use a gate engine to start/stop the rotation of // the bigger duck. bigDuckGate = new SoGate(typeof(SoMFFloat)); bigDuckTime = new SoElapsedTime(); bigDuckGate.input.ConnectFrom(bigDuckTime.timeOut); bigDuckRotXYZ.axis.Value = SoRotationXYZ.AxisType.Y; // Y axis bigDuckRotXYZ.angle.ConnectFrom(bigDuckGate.output); // Each mouse button press will enable/disable the gate // controlling the bigger duck. SoEventCallback myEventCB = new SoEventCallback(); myEventCB.AddEventCallback(typeof(SoMouseButtonEvent), myMousePressCB); root.AddChild(myEventCB); // Use a Boolean engine to make the rotation of the smaller // duck depend on the bigger duck. The smaller duck moves // only when the bigger duck is still. myBoolean = new SoBoolOperation(); myBoolean.a.ConnectFrom(bigDuckGate.enable); myBoolean.operation.SetValue(SoBoolOperation.Operations.NOT_A); smallDuckGate = new SoGate(typeof(SoMFFloat)); smallDuckTime = new SoElapsedTime(); smallDuckGate.input.ConnectFrom(smallDuckTime.timeOut); smallDuckGate.enable.ConnectFrom(myBoolean.output); smallDuckRotXYZ.axis.Value = SoRotationXYZ.AxisType.Y; // Y axis smallDuckRotXYZ.angle.ConnectFrom(smallDuckGate.output);
// Bigger duck group SoSeparator bigDuck = new SoSeparator(); SoRotationXYZ bigDuckRotXYZ = new SoRotationXYZ(); SoTransform bigInitialTransform = new SoTransform(); bigInitialTransform.translation.setValue(0.0f, 0.0f, 3.5f); bigInitialTransform.scaleFactor.setValue(6.0f, 6.0f, 6.0f); { bigDuck.addChild(bigDuckRotXYZ); bigDuck.addChild(bigInitialTransform); bigDuck.addChild(duckObject); } // Smaller duck group SoSeparator smallDuck = new SoSeparator(); SoRotationXYZ smallDuckRotXYZ = new SoRotationXYZ(); SoTransform smallInitialTransform = new SoTransform(); smallInitialTransform.translation.setValue(0.0f, -2.24f, 1.5f); smallInitialTransform.scaleFactor.setValue(4.0f, 4.0f, 4.0f); { smallDuck.addChild(smallDuckRotXYZ); smallDuck.addChild(smallInitialTransform); smallDuck.addChild(duckObject); } // Use a gate engine to start/stop the rotation of // the bigger duck. SoEventCallback myEventCB = new SoEventCallback(); SoBoolOperation myBoolean = new SoBoolOperation(); try { SoGate bigDuckGate = new SoGate(SoMFFloat.class); SoElapsedTime bigDuckTime = new SoElapsedTime(); bigDuckGate.input.connectFrom(bigDuckTime.timeOut); bigDuckRotXYZ.axis.setValue(SoRotationXYZ.AxisType.Y); // Y axis bigDuckRotXYZ.angle.connectFrom(bigDuckGate.output); // Each mouse button press will enable/disable the gate // controlling the bigger duck. myEventCB.addEventCallback(SoMouseButtonEvent.class, new MousePressCB(bigDuckGate)); // Use a Boolean engine to make the rotation of the smaller // duck depend on the bigger duck. The smaller duck moves // only when the bigger duck is still. myBoolean.a.connectFrom(bigDuckGate.enable); myBoolean.operation.setValue(SoBoolOperation.Operations.NOT_A.getValue()); } catch (Exception e) { e.printStackTrace(); } try { SoGate smallDuckGate = new SoGate(SoMFFloat.class); SoElapsedTime smallDuckTime = new SoElapsedTime(); smallDuckGate.input.connectFrom(smallDuckTime.timeOut); smallDuckGate.enable.connectFrom(myBoolean.output); smallDuckRotXYZ.axis.setValue(SoRotationXYZ.AxisType.Y); // Y axis smallDuckRotXYZ.angle.connectFrom(smallDuckGate.output); } catch (Exception e) { e.printStackTrace(); }
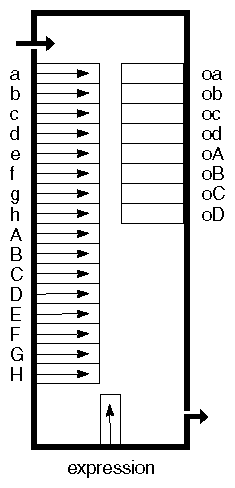
The calculator engine, SoCalculator SoCalculator SoCalculator , is similar to the Boolean engine, but it handles a wider range of operations and has more inputs and outputs. As shown in Figure 15.16, “ SoCalculator Engine ”, this engine has the following inputs and outputs:
|
Inputs |
SoMFFloat |
a, b, c, d, e, f, g, h |
|
|
SoMFVec3f |
A, B, C, D, E, F, G, H |
|
|
SoMFString |
expression |
|
|
|
|
|
Outputs |
SoEngineOutput |
oa, ob, oc, od (SoMFFloat) |
|
|
SoEngineOutput |
oA, oB, oC, oD (SoMFVec3f) |
The expression input, shown at the bottom of the engine, is of type SoMFString SoMFString SoMFString and is of the form:
“lhs = rhs”
lhs (lefthand side) can be any one of the outputs or a temporary variable. This engine provides eight temporary floating-point variables (ta – th) and eight temporary vector variables (tA – tH).
rhs (righthand side) supports the following operators:
|
Type of Operator |
Example |
|---|---|
|
Binary operators |
+ - * / < > >= <= == != && || |
|
Unary operators |
- ! |
|
Ternary operator |
cond ? trueexpr : falseexpr |
|
Parentheses |
( expr ) |
|
Vector indexing |
vec [int] |
|
Functions |
func( expr, ... ) |
|
Terms |
integer or floating-point constants; named constants such as MAXFLOAT, MINFLOAT, M_LOG2E, M_PI; the names of the calculator engine's inputs, outputs, and temporary variables (a, b, A, B, oa, ob, ta, tb, tA, tB, and so on) |
See the Open Inventor C++ Reference Manual for detailed information on using these operators.
Here is a simple example of using the calculator engine. It uses the following inputs and outputs:
|
Inputs |
Outputs |
|---|---|
|
2 vectors (A, B) |
oA (f times the negation of the cross product of A and B) |
|
2 scalars (a, f) |
oa (convert a from degrees to radians) |
To specify the expression for a calculator engine called calc, the code would be
calc->expression.set1Value(0, "oa = a * M_PI / 180"); calc->expression.set1Value(1, "oA = -f * cross(A, B)");
calc.expression[0] = "oa = a * M_PI / 180"; calc.expression[1] = "oA = -f * cross(A, B)";
calc.expression.set1Value(0, "oa = a * M_PI / 180"); calc.expression.set1Value(1, "oA = -f * cross(A, B)");
Multiple expressions are evaluated in order, so a variable assigned a value in an earlier expression can be used in the righthand side of a later expression. Several expressions can be specified in one string, separated by semicolons.
The expressions can also operate on arrays. If one input contains fewer values than another input, the last value is replicated as necessary to fill out the array. All the expressions will be applied to all elements of the arrays. For example, if input a contains multiple values and input b contains the value 1.0, then the expression “oa = a + b” will add 1 to all of the elements in a.
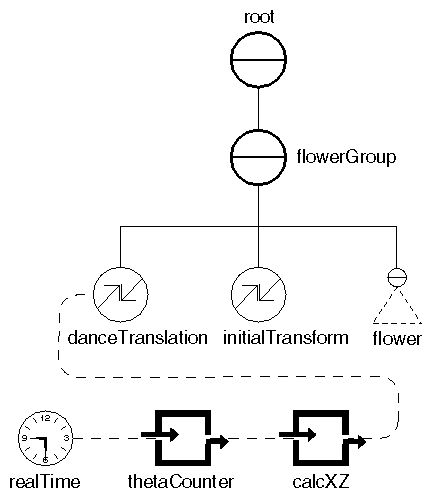
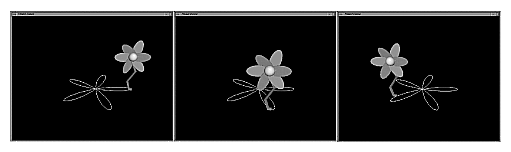
Example 15.6, “ Using a Calculator Engine ” shows using the calculator engine to move a flower along a path. The calculator engine computes a closed, planar curve. The output of the engine is connected to the translation applied to a flower object, which then moves along the path of the curve. Figure 15.17, “ Scene Graph for Calculator Engine Example ” shows the scene graph for this example. The dancing flower is shown in Figure 15.18, “ Using a Calculator Engine to Constrain an Object's Movement ”.
Example 15.6. Using a Calculator Engine
// Flower group
SoSeparator *flowerGroup = new SoSeparator;
root->addChild(flowerGroup);
// Read the flower object from a file and add to the group
if (!myInput.openFile("flower.iv"))
exit(1);
SoSeparator *flower= SoDB::readAll(&myInput);
if (flower == NULL)
exit(1);
// Set up the flower transformations
SoTranslation *danceTranslation = new SoTranslation;
SoTransform *initialTransform = new SoTransform;
flowerGroup->addChild(danceTranslation);
initialTransform->scaleFactor.setValue(10., 10., 10.);
initialTransform->translation.setValue(0., 0., 5.);
flowerGroup->addChild(initialTransform);
flowerGroup->addChild(flower);
// Flower group
SoSeparator flowerGroup = new SoSeparator();
root.AddChild(flowerGroup);
// Read the flower object from a file and add to the group
myInput.OpenFile("../../../../../data/flower.iv");
SoSeparator flower = SoDB.ReadAll(myInput);
// Set up the flower transformations
SoTranslation danceTranslation = new SoTranslation();
SoTransform initialTransform = new SoTransform();
flowerGroup.AddChild(danceTranslation);
initialTransform.scaleFactor.SetValue(10.0f, 10.0f, 10.0f);
initialTransform.translation.SetValue(0.0f, 0.0f, 5.0f);
flowerGroup.AddChild(initialTransform);
flowerGroup.AddChild(flower);
// Flower group
SoSeparator flowerGroup = new SoSeparator();
root.addChild(flowerGroup);
// Read the flower object from a file and add to the group
myInput.openFile("../../../../../data/flower.iv");
SoSeparator flower = SoDB.readAll(myInput);
// Set up the flower transformations
SoTranslation danceTranslation = new SoTranslation();
SoTransform initialTransform = new SoTransform();
flowerGroup.addChild(danceTranslation);
initialTransform.scaleFactor.setValue(10.0f, 10.0f, 10.0f);
initialTransform.translation.setValue(0.0f, 0.0f, 5.0f);
flowerGroup.addChild(initialTransform);
flowerGroup.addChild(flower);
// Set up an engine to calculate the motion path: // r = 5*cos(5*theta); x = r*cos(theta); z = r*sin(theta) // Theta is incremented using a time counter engine, // and converted to radians using an expression in // the calculator engine. SoCalculator *calcXZ = new SoCalculator; SoTimeCounter *thetaCounter = new SoTimeCounter; thetaCounter->max = 360; thetaCounter->step = 4; thetaCounter->frequency = 0.075; calcXZ->a.connectFrom(&thetaCounter->output); calcXZ->expression.set1Value(0, "ta=a*M_PI/180"); // theta calcXZ->expression.set1Value(1, "tb=5*cos(5*ta)"); // r calcXZ->expression.set1Value(2, "td=tb*cos(ta)"); // x calcXZ->expression.set1Value(3, "te=tb*sin(ta)"); // z calcXZ->expression.set1Value(4, "oA=vec3f(td,0,te)"); danceTranslation->translation.connectFrom(&calcXZ->oA);
// Set up an engine to calculate the motion path: // r = 5*cos(5*theta); x = r*cos(theta); z = r*sin(theta) // Theta is incremented using a time counter engine, // and converted to radians using an expression in // the calculator engine. calcXZ = new SoCalculator(); thetaCounter = new SoTimeCounter(); thetaCounter.max.Value = (360); thetaCounter.step.Value = (4); thetaCounter.frequency.Value = (0.075f); calcXZ.a.ConnectFrom(thetaCounter.output); calcXZ.expression[0] = "ta=a*M_PI/180"; // theta calcXZ.expression[1] = "tb=5*cos(5*ta)"; // r calcXZ.expression[2] = "td=tb*cos(ta)"; // x calcXZ.expression[3] = "te=tb*sin(ta)"; // z calcXZ.expression[4] = "oA=vec3f(td,0,te)"; danceTranslation.translation.ConnectFrom(calcXZ.oA);
thetaCounter.max.setValue((short)360); thetaCounter.step.setValue((short)4); thetaCounter.frequency.setValue(0.075f); calcXZ.a.connectFrom(thetaCounter.output); calcXZ.expression.set1Value(0, "ta=a*M_PI/180"); // theta calcXZ.expression.set1Value(1, "tb=5*cos(5*ta)"); // r calcXZ.expression.set1Value(2, "td=tb*cos(ta)"); // x calcXZ.expression.set1Value(3, "te=tb*sin(ta)"); // z calcXZ.expression.set1Value(4, "oA=vec3f(td,0,te)"); danceTranslation.translation.connectFrom(calcXZ.oA);