SoAlgebraicShape Class Reference
[Shapes]

Abstract base class for algebraic shapes. More...

#include <Inventor/nodes/SoAlgebraicShape.h>

Inheritance diagram for SoAlgebraicShape:

Public Types
enum	ASWorkSpace { BOX, CAMERA, WORLD, MAX_WORK_SPACE }
enum	ASShaderSlot { COMPUTE_COLOR, VERTEX_SHADER_ENTRY, MAX_SHADER_SLOT }
enum	ASClippingPolicy { STANDARD, FULL_SHAPE }
Public Member Functions
virtual SoType	getTypeId () const
Static Public Member Functions
static SoType	getClassTypeId ()
Public Attributes
SoSFNode	rayIntersection
SoSFEnum	workspace
SoMFNode	shaderSlots
SoSFBool	generateTransparency
SoSFEnum	clippingPolicy

Detailed Description

Abstract base class for algebraic shapes.

An implicit surface is a 2-dimensional surface in 3-dimensional space defined as the locus of zeros of a given function. Many useful shapes such as sphere, cylinder or cone can be expressed using this approach, known as a quadric surfaces.

Sub-classes of this node compute and render an implicit surface on the GPU using a GLSL shader function. A screen-aligned quad is drawn, representing the screen space bounding box of the algebraic shape. Then, this quad is ray-casted and a ray/shape intersection is applied per fragment to draw the final shape.

Several predefined sub-classes are provided for convenience, including SoAlgebraicCone, SoAlgebraicCylinder and SoAlgebraicSphere. These nodes can be used in an application scene graph similar to the corresponding classic geometry nodes SoCone, SoCylinder and SoSphere. Use a transform node, e.g. SoTransform, to position the shape node in 3D space. Use an SoMaterial node to assign material properties. See the notes and limitations section on this page for some important differences between algebraic and geometric shapes.

Extending SoAlgebraicShape:

Derived classes must implement the bounding box computation function computeBBox() in C++. And also implement the ray/shape intersection function OivASRayIntersection() in GLSL. This function returns true if there is an intersection between the ray and the shape, false otherwise. Create an SoFragmentShader to hold the GLSL function and set this node in the rayIntersection field.


   bool
   OivASRayIntersection ( in OivASRay ray, inout OivASPoint point )
   {
      DO SOMETHING
      return [ true | false ];
   }

See the GLSL include file oivAlgebraicShape.h in $OIVHOME/shaders/include/Inventor/AlgebraicShape. It declares ray, a structure that contains ray parameters:

  struct OivASRay {
    vec3 rs; // ray start
    vec3 re; // ray end
    vec3 rd; // ray direction
  };

and point, an output structure containing position, normal and color (if any) of the intersection point.

  struct OivASPoint {
    vec3 position;
    vec3 normal;
    vec4 color;
  };

Note that ray parameters and point information are defined in the reference frame specified by the workspace field, an enum of type ASWorkSpace. This frame can be the camera space, the world space or the normalized space of the bounding box of the shape. By default, the bounding box space is used.

A GLSL helper function for solving quadratic functions (i.e. a*x^2 + b*x + c = 0) is provided:

   bool OivASSolveQuadric ( in vec3 abc, inout vec2 roots );

with abc, a vector containing the coefficients {a, b, c} of the polynomial. A quadratic equation has zero, one or two solutions, called roots. It returns true if there are solutions, false otherwise. Note that only helper function for quadric surfaces are provided but higher order surface such as Torus (i.e. degree 4) may be implemented using user-defined polynomial solver.

All quadric shape equations can be solved using this function. For instance, the equation of a sphere centered at the origin with a radius of 1 is defined by:

$\begin{equation} x^2 + y^2 + z^2 - 1 = 0 \end{equation}$

To find the intersection point between such a sphere with a ray as defined above, we have to solve the quadric sphere equation such as:

$\begin{equation} (rs + t*rd)^2 - 1 = 0 \end{equation}$

which leads to,

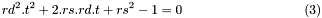
$\begin{equation} rd^2 . t^2 + 2 . rs . rd . t + rs^2 - 1 = 0 \end{equation}$

It means solving a quadratic equation with:

a = 1 (i.e. dot(rd, rd) = 1),
b = 2 * dot(rs, rd),
c = dot(rs, rs) - 1.0.

If a solution exists (1 or 2), the OivASSolveQuadric function returns true and roots are stored in the parameter roots. The roots (i.e. t1 and t2) represent the solution for the parameter t such as solutions are:

p1 = rs + t1*rd
p2 = rs + t2*rd

The smallest positive root is the first intersection point along the ray direction rd. If there are two positive roots, the larger one is the intersection point with the back face. If a root is negative, it means that there is an intersection in the opposite ray direction.

While this node is designed to address algebraic surfaces, the ray intersection function could be used with other types of surfaces to find the intersection between the ray and the shape (e.g. distance functions).

Note that this node supports instancing using SoMultipleInstance to render millions of algebraic shapes in a more efficient way than than using geometric shapes.

The application can also provide custom color shaders to shade the surface or use built-in shading based on light model and material properties (transparency is supported as well).

Notes:

Shape hints (SoShapeHints) do not affect rendering.
Algebraic shapes are always rendered as if "two-sided lighting" is enabled.
Complexity (SoComplexity) does not affect rendering.
Algebraic shapes are not tessellated, so are always "full resolution".
Material binding (SoMaterialBinding) does not affect rendering.
(You can't color the caps differently like you can with SoCylinder, etc.)
Algebraic shapes can be picked, but no SoDetail is available.
Wireframe rendering is not supported since this node does not generate real geometry.

Limitations:

Texturing (SoTexture2) does not affect rendering.
Projection (SoProjection) does not affect rendering.
Draw style (SoDrawStyle) does affect rendering,
but the result is a single line segment, not a wire frame shape.

See also:: SoAlgebraicSphere, SoAlgebraicCylinder, SoAlgebraicCone

See related examples:: CustomAlgebraicShape, CustomComputeColor, MultiInstancingAlgebraicShape

Member Enumeration Documentation

enum SoAlgebraicShape::ASClippingPolicy

Specifies how the algebraic shape should be clipped by a clipping plane.

Enumerator:

STANDARD

FULL_SHAPE

Standard behaviour.

The shape can be partially clipped by the clipping plane.

enum SoAlgebraicShape::ASShaderSlot

Specifies the available slots for shader programs.

Enumerator:

COMPUTE_COLOR
VERTEX_SHADER_ENTRY
MAX_SHADER_SLOT

enum SoAlgebraicShape::ASWorkSpace

Specifies which reference frame to use inside the ray intersection shader function.

Enumerator:

BOX
CAMERA	The normalized bounding box space.
WORLD	The camera space (or view space).
MAX_WORK_SPACE	The world space.

Member Function Documentation

static SoType SoAlgebraicShape::getClassTypeId ( ) [static]

Returns the type identifier for this class.

Reimplemented from SoShape.

Reimplemented in SoAlgebraicCone, SoAlgebraicCylinder, and SoAlgebraicSphere.

virtual SoType SoAlgebraicShape::getTypeId ( ) const [virtual]

Returns the type identifier for this specific instance.

Reimplemented from SoShape.

Reimplemented in SoAlgebraicCone, SoAlgebraicCylinder, and SoAlgebraicSphere.

Member Data Documentation

SoSFEnum SoAlgebraicShape::clippingPolicy

Specifies how the algebraic shape should be clipped by a clipping plane.

Default value is STANDARD.

SoSFBool SoAlgebraicShape::generateTransparency

Specify if the shape generates transparent fragment.

This field is similar to the one in SoShaderProgram. If set to true, the shape is considered as transparent. Otherwise, the shape transparency is deducted from the state. Note that this flag is useful is you want to generate transparent color from custom computer color shader slot without binding a material node.

Default value is FALSE.

See also:: SoShaderProgram

SoSFNode SoAlgebraicShape::rayIntersection

Field for an SoFragmentShader object that defines the GLSL ray intersection function.

The GLSL function must compute the intersection between a ray and the shape. Note that position and direction space is chosen according to the value of workspace. This function must be implemented as:


   bool
   OivASRayIntersection ( in OivASRay ray, inout OivASPoint p )
   {
      DO SOMETHING
      return [ true | false ];
   }

SoMFNode SoAlgebraicShape::shaderSlots

Multi-field for Shader slots of type SoShaderObject.

Shader slots can contain application provided shader functions and are of the type defined in ASShaderSlot enumeration:

COMPUTE_COLOR [optional] is the slot corresponding to the fragment color shading computation. The position and normal defined in the OivASPoint structure are expressed in camera space. Function must be defined as:


   vec4 OivASComputeColor ( in OivASPoint p )
   {
      DO SOMETHING
      return A_COLOR;
   }

VERTEX_SHADER_ENTRY [optional] is the slot corresponding to vertex shader entry point for initializing varying parameters from attributes (e.g. mesh attributes or instance parameters). Function must be defined as:


   void OivASVertexShaderEntry ()
   {
      DO SOMETHING
   }

SoSFEnum SoAlgebraicShape::workspace

Field to define the workspace.

Use enum ASWorkSpace. Default is BOX.

Possible choices are:

BOX [default], where positions and directions are expressed in the normalized bounding box space i.e. the center of the box is (0.0, 0.0, 0.0) and axes are the box axes.

CAMERA, where positions and directions are expressed in the view space.

WORLD, where positions and directions are expressed in the world space.

The documentation for this class was generated from the following file:

Inventor/nodes/SoAlgebraicShape.h

SoAlgebraicShape Class Reference [Shapes]

Public Types

Public Member Functions

Static Public Member Functions

Public Attributes

Detailed Description

Member Enumeration Documentation

Member Function Documentation

Member Data Documentation

SoAlgebraicShape Class Reference
[Shapes]