Package com.openinventor.imageviz.engines.imageanalysis.globalmeasures

Class SoCurvatureIntegralsQuantification3d

  • All Implemented Interfaces:
    SafeDisposable
    public class SoCurvatureIntegralsQuantification3d
extends SoImageVizEngine
    SoCurvatureIntegralsQuantification3d engine computes the integral of mean curvature and integral of total curvature. For an introduction, see section Analysis.

    This engine computes the integral of mean curvature and integral of total curvature of objects in a binary image. Intuitively, "curvature" is the amount by which a geometric object deviates from being "flat".

    This engine computes a local measure. It is obtained as the sum of measures in local 2x2x2 neighborhoods (a cube), for 13 planes associated with different normal directions and hitting three or four vertices of the cells (in the cubical lattice).

    In the case of very elongated objects (needles or fibers) the integral of mean curvature 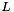can be used to measure the length 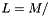of the object :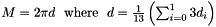

    For convex object, the integral of mean curvature 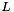is (up to a constant) equivalent to the mean diameter, i.e.

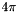
    The Euler number and the Integral of Total Curvature carry the same information about the object. They differ by the constant factor 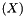. If we consider a set X of the 3-dimensional space and 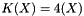being its Euler number then the integral total curvature of X will be : .

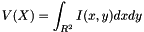    For more information on Integral Curvatures you can refer to C .Lang, J. Ohser, R.Hilfer (1999) On the Analysis of Spatial Binary Images

    File format/default:

    CurvatureIntegralsQuantification3d {

      inImage NULL
    }


    Library references: integral_curvature