The GraphMaster class library extends Open Inventor capabilities in the following three areas:
2D drawing : With this first set of extensions, you can design your 2D graphics applications very easily and efficiently. This includes simple 2D shapes, such as rectangles, circles, and arrows, 2D charting nodes to draw a large range of different 2D axes (linear, logarithmic, angular, time, etc.), curves and markers fields, statistical nodes using pie or bar chart representations, error areas, high-low-close curves, and so forth.
3D drawing : The previous classes are extended to 3D in order to provide features such as 3D circles, 3D pie or bar charts, 3D curves, and 3D axes. These nodes give you access to a wide range of new 3D functionality.
Legends : A wide variety of legends is provided to annotate your visualizations.
Before going any further, it is very important to read Section 2.1, “ What You Must Know about MeshViz XLM: ”, mainly for the reminder about node kits and the explanation of the GraphMaster and 3DdataMaster domain facilities.
GraphMaster introduces the following 2D and 3D classes that complement the Open Inventor 3D shape node set:

All the above are node kits and have one appearance part that allows the application to change the appearance (material, draw style, texture, etc.) of each of them. The PoArrow( C++ | Java | .NET )and PoArrow3( C++ | Java | .NET )nodes, however, have three appearance parts that allow for the control of the starting shape of the arrow, the ending shape, and the line of the arrow. All angles are specified in radians. Refer to the reference manual for a full description of node kit parts and node fields. The following example (located in $OIVHOME/src/MeshViz/Mentor) shows how to create an arrow and set the appearance of the parts. Note that the domain functionality is important for PoArrow( C++ | Java | .NET )and PoArrow3( C++ | Java | .NET )nodes since the length and width of the starting and ending patterns are given as percentages of the domain (as a reminder, the default domain is [0,1] × [0,1] × [0,1], and default pattern widths and heights are 5% of the domain).
Example 2.13. Drawing an arrow
C++
// tutorialGraph01.cxx ... // Create the root of the scene graph SoAnnotation *root = new SoAnnotation; root->ref(); // Create the arrow and set appearance PoArrow *myArrow = new PoArrow; SbVec2f points[3]= {SbVec2f(0.,0.), SbVec2f(10.,10.), SbVec2f(20.,10.) }; myArrow->point.setValues(0,3,points); myArrow->endPatternType = PoArrow::DIRECT_TRIANGLE; myArrow->set("endApp.material","diffuseColor 1 0 0"); myArrow->set("appearance.material", "diffuseColor 0 0 0"); myArrow->patternWidth = .1; myArrow->patternHeight = .075; // Set the domain to define end pattern size #ifdef USE_PB PbDomain myDom(0.,0.,20.,20.); myArrow->setDomain(&myDom); #else PoDomain *myDom = new PoDomain; myDom->min = SbVec3f(0,0,0); myDom->max = SbVec3f(20,20,0); root->addChild(myDom); #endif root->addChild(myArrow); SoXtPlaneViewer *viewer = new SoXtPlaneViewer(myWindow); viewer->setSceneGraph(root); viewer->setBackgroundColor(SbColor(1., 1., 1.)); ...
GraphMaster provides the following 2D and 3D classes that give you access to a whole new set of features for designing business graphics visualizations, such as curves, high-low-close curves, error bars, axes and axis systems, bar charts, legends, and more. (The indentation shows class derivations; you will notice that all classes are derived from PoGraphMaster( C++ | Java | .NET ) ):
PoCurve( C++ | Java | .NET )and PoCurve3( C++ | Java | .NET )are the two classes used to draw curves in 2D or 3D. PoCurve( C++ | Java | .NET ) builds a curve in the XY plane and may use different representations depending on the curveRepfield. This representation may be a standard polyline joining the given points, a smooth curve, a stair curve, etc. The area between the curve and a given threshold may be filled. “Raised” points can be added to the visualization, as well as markers to identify the location of points on the curve. The 3D class PoCurve3( C++ | Java | .NET )only supports polyline and smooth representations.
The following example (located in $OIVHOME/src/MeshViz/Mentor) creates a curve (sine curve) and shows different attributes that can be used to change the visualization:
Example 2.14. A curve and its attributes
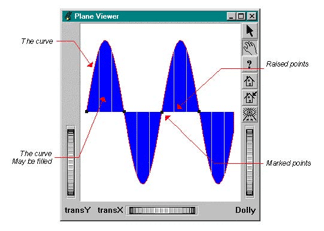
C++
//tutorialGraph02.cxx ... // Create the root of the scene graph SoAnnotation *root = new SoAnnotation; root->ref(); // Create the curve PoCurve *myCurve = new PoCurve; #define N_PT 50 #define PI 3.1415 SbVec2f points[N_PT]; double ang; int i; for (i=0, ang=0.; i < N_PT; i++, ang += 4.*PI/(double)N_PT) points[i].setValue(ang, 6. * sin(ang)); myCurve->point.setValues(0,N_PT,points); myCurve->curveRep = PoCurve::CURVE_POLYLINE; myCurve->isCurveFilled = TRUE; myCurve->raiseFilterType = PoCurve::X_PERIOD; myCurve->raiseXPeriod = PI/3.; myCurve->raiseThreshold = 0.0; myCurve->markerFilterType = PoCurve::X_PERIOD; myCurve->markerXPeriod = PI; myCurve->set("markerApp.material", "diffuseColor [0 0 0]"); myCurve->set("markerApp.drawStyle", "pointSize 5.0"); myCurve->set("curvePointApp.material", "diffuseColor [1 0 0]"); myCurve->set("curveFillingApp.material", "diffuseColor [0 0 1]"); root->addChild(myCurve); SoXtPlaneViewer *viewer = new SoXtPlaneViewer(myWindow); viewer->setSceneGraph(root); viewer->setBackgroundColor(SbColor(1., 1., 1.)); ...
Now, we may want to add axes to our curve in order to make the visualization more meaningful. GraphMaster provides a wide range of axes: Cartesian, polar or angular, linear, logarithmic, generalized, and time axes. GraphMaster also provides axis system nodes that are able to maintain “boxes” of 2, 3, 4, or 6 axes, or sets of axes where axes are defined on a parallelepiped related to the view. The axis classes are as follows (indentation shows class derivations):
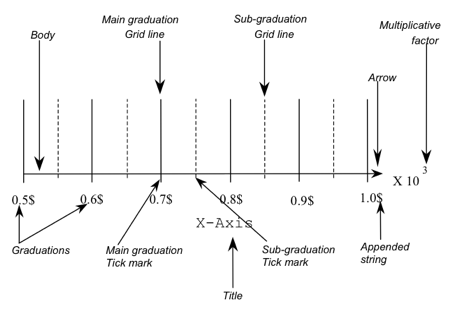
All axes will be drawn using a default representation if none is specified by the application. This means that depending on the domain, GraphMaster will compute the tick locations, text height, and so on, in order to generate a good default visualization.
gradVisibility : to switch graduation visibility on and off.
gradPath : to set the graduation path to be up, down, left, or right.
gradFontName : to change the default font used to draw graduations.

gradDistAxis : to specify the spacing between the graduations and the axis main line (relative to the domain).
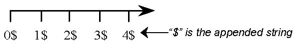
gradAddStringVisibility : an appended string may be added to each graduation (to specify a unit, for example).
titleVisibility : to switch the title visibility on and off.
titlePosition : to draw the title in the middle or at the end of the axis.
titlePath : to set the title path to be up, down, left, or right.
titleFontName : to change the default font used to draw the title.
titleDistAxis : to specify the spacing between the title and the axis main line (relative to the domain).
tickPosition : to specify which side of the axis ticks are to be drawn on.
tickSubLength : sub-tick line length (relative to the domain).
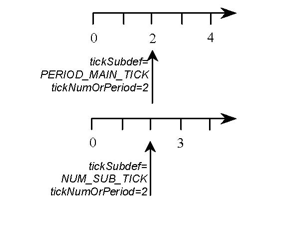
tickSubDef : to specify if tickNumOrPeriodfield indicates the number of sub-graduations between two main graduations (NUM_SUB_TICK) or the period used to draw the graduations associated with the main tick (PERIOD_MAIN_TICK).
tickNumOrPeriod : to define the value associated with the previous field. If tickSubDefis NUM_SUB_TICK and tickNumOrPeriodis 2, then two sub-ticks are drawn between two subsequent main ticks. If tickSubDefis PERIOD_MAIN_TICK and tickNumOrPeriodis 3, then no sub-ticks are drawn and only one main tick every three main ticks will be annotated with a graduation.
![[Note]](../../images/note.jpg) | |
GraphMaster objects are node kits (see the section called “ Visualization classes”), so you can access each part and change the appearance of each of them. Many axis attributes are computed relative to the domain (see Section 2.1, “ What You Must Know about MeshViz XLM: ”). Text height, arrow length and width, number of ticks, height of ticks, etc. are all computed automatically by GraphMaster (if the field is <= 0.) relative to the domain if your application does not provide a value. All Cartesian and polar axes have geometric starting and ending points. These points are used to compute the location of the axes on the display. For an angular axis, the axis is always centered, when built, at point (0,0,0). |
The following example (located in $OIVHOME/src/MeshViz/Mentor) uses Example 2.14, “ A curve and its attributes”, but the curve representation now keeps only the polyline and gets rid of the fill, and the raised and marked points. We are going to use two Cartesian linear axes and add them to our curve to get a new visualization.
Example 2.15. A curve which keeps only the polyline
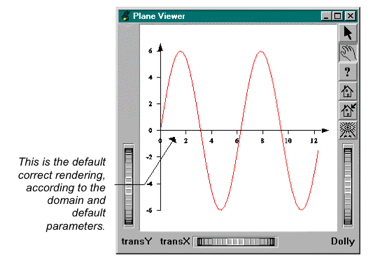
C++
// tutorialGraph03.cxx ... // Create the curve PoCurve *myCurve = new PoCurve; SbVec2f points[N_PT]; double ang; int i; for (i=0, ang=0.; i < N_PT; i++, ang += 4.*PI/(double)N_PT) points[i].setValue(ang, 6. * sin(ang)); myCurve->point.setValues(0,N_PT,points); myCurve->set("curvePointApp.material", "diffuseColor [1 0 0]"); // Create simple automatic X and Y linear axis // Do not forget to set the domain if you want // default parameters to be correct... PoLinearAxis *myXAxis = new PoLinearAxis; myXAxis->start.setValue(SbVec3f(0.,0.,0.)); myXAxis->end = 4.*PI; myXAxis->type = PoCartesianAxis::XY; myXAxis->set("appearance.material", "diffuseColor 0 0 0"); PoLinearAxis *myYAxis = new PoLinearAxis; myYAxis->start.setValue(SbVec3f(0.,-6.,0.)); myYAxis->end = 6.; myYAxis->type = PoCartesianAxis::YX; myYAxis->set("appearance.material", "diffuseColor 0 0 0"); // Create the root of the scene graph SoSeparator *root = new SoSeparator; root->ref(); // Define domain #ifdef USE_PB PbDomain myDom(0.,-6.,4.*PI,6.); myXAxis->setDomain(&myDom); myYAxis->setDomain(&myDom); myCurve->setDomain(&myDom); #else PoDomain *myDom = new PoDomain; myDom->min = SbVec3f(0,-6,0); myDom->max = SbVec3f(4.*PI,6.,0); root->addChild(myDom); #endif root->addChild(myXAxis); root->addChild(myYAxis); root->addChild(myCurve); SoXtPlaneViewer *viewer = new SoXtPlaneViewer(myWindow); viewer->setSceneGraph(root); viewer->setBackgroundColor(SbColor(1., 1., 1.)); ...
We perhaps want the axes to share the same origin, and not to cross each other. To make this, we simply have to change the origin of our X axis:
C++
myXAxis->start.setValue(SbVec3f(0.,-6.,0.));
Example 2.16. Curve and axes with grid lines and sub-graduations
C++
... // Create simple automatic X and Y linear axis // Do not forget to set the domain if you want // default parameters to be correct... PoLinearAxis *myXAxis = new PoLinearAxis; myXAxis->start.setValue(SbVec3f(0.,-6.,0.)); myXAxis->end = 4.*PI; myXAxis->step = 1.; myXAxis->type = PoCartesianAxis::XY; myXAxis->gridVisibility = PoAxis::VISIBILITY_ON; myXAxis->gridLengthGradOtherSide = 12; myXAxis->tickSubDef = PoAxis::PERIOD_MAIN_TICK; myXAxis->setDomain(&myDom); root->addChild(myXAxis); PoLinearAxis *myYAxis = new PoLinearAxis; myYAxis->start.setValue(SbVec3f(0.,-6.,0.)); myYAxis->end = 6.; myYAxis->type = PoCartesianAxis::YX; myYAxis->gridVisibility = PoAxis::VISIBILITY_ON; myYAxis->gridLengthGradOtherSide = 4.*PI; myYAxis->tickSubDef = PoAxis::NUM_SUB_TICK; myYAxis->tickNumOrPeriod = 2; myYAxis->setDomain(&myDom); root->addChild(myYAxis); ...
![[Important]](../../images/important.jpg) | |
Notice that the grid lines are drawn on top of the curve. This is because of the traversal order of the scene graph: the curve object is traversed (thus drawn) before the axes. If you prefer to have the curve drawn on top of the grid, just add the curve to the scene graph after adding the axes. |
Instead of creating two PoLinearAxis( C++ | Java | .NET )nodes we could have chosen to use a group of axes. GraphMaster provides five classes to deal directly with “boxes” of axes (2D and 3D axes):
The following program (located in $OIVHOME/src/MeshViz/Mentor) draws the same curve but this time using a PoGroup2Axis( C++ | Java | .NET )node. You will notice in this example that each individual axis may be customized in the same way as in the previous example. To do this, all you have to do is get the part corresponding to the axis in the PoGroup2Axis( C++ | Java | .NET )node kit using the SO_GET_PARTOpen Inventor macro and then edit whatever field you want on this specific axis:
Example 2.17. Using a group of axes
C++
// tutorialGraph04.cxx ... // Create the curve PoCurve *myCurve = new PoCurve; SbVec2f points[N_PT]; double ang; int i; for (i=0, ang=0.; i < N_PT; i++, ang += 4.*PI/(double)N_PT) points[i].setValue(ang, 6. * sin(ang)); myCurve->point.setValues(0,N_PT,points); myCurve->set("curvePointApp.material", "diffuseColor [1 0 0]"); // Create a group of 2 axis and edit some fields of them PoGroup2Axis *my2Axis = new PoGroup2Axis; my2Axis->start.setValue(SbVec2f(0.,-6.)); my2Axis->end.setValue(SbVec2f(4.*PI,6.)); my2Axis->xTitle = "Y=Sin(X)"; my2Axis->set("appearance.material", "diffuseColor 0 0 0"); PoLinearAxis *myXAxis = SO_GET_PART(my2Axis, "xAxis", PoLinearAxis); PoLinearAxis *myYAxis = SO_GET_PART(my2Axis, "yAxis", PoLinearAxis); myXAxis->step = 1.; myYAxis->tickSubDef = PoAxis::NUM_SUB_TICK; myYAxis->tickNumOrPeriod = 2; // Create the root of the scene graph SoSeparator *root = new SoSeparator; root->ref(); #ifdef USE_PB // Define domain PbDomain myDom(0.,-6.,4.*PI,6.); myCurve->setDomain(&myDom); my2Axis->setDomain(&myDom); #else PoDomain *myDom = new PoDomain; myDom->min = SbVec3f(0,-6,0); myDom->max = SbVec3f(4.*PI,6.,0); root->addChild(myDom); #endif root->addChild(my2Axis); root->addChild(myCurve); SoXtPlaneViewer *viewer = new SoXtPlaneViewer(myWindow); viewer->setSceneGraph(root); viewer->setBackgroundColor(SbColor(1., 1., 1.)); ...
Several curves may also share the same axis system. The following example (located in $OIVHOME/src/MeshViz/Mentor) draws two curves sharing the same PoGroup2Axis( C++ | Java | .NET ) node.
![[Tip]](../../images/tip.jpg) | |
Refer to the section called “ Step 4: Multiple curves sharing one X axis and different Y axes”, if you want to draw several curves that do not share the same axis system. |
Example 2.18. Two curves sharing the same axes
C++
// tutorialGraph05.cxx ... // Create the curves double ang; int i; SbVec2f points1[N_PT]; PoCurve *myCurve1 = new PoCurve; for (i=0, ang=0.; i < N_PT; i++, ang += 4.*PI/(double)N_PT) points1[i].setValue(ang, 6. * sin(ang)); myCurve1->point.setValues(0,N_PT,points1); myCurve1->set("curvePointApp.material", "diffuseColor [1 0 0]"); SbVec2f points2[N_PT]; PoCurve *myCurve2 = new PoCurve; for (i=0, ang=0.; i < N_PT; i++, ang += 4.*PI/(double)N_PT) points2[i].setValue(ang, PI * cos(ang)); myCurve2->point.setValues(0,N_PT,points2); myCurve2->set("curvePointApp.material", "diffuseColor [0 1 0]"); // Create a group of 2 axis and edit some fields of them PoGroup2Axis *my2Axis = new PoGroup2Axis; my2Axis->set("appearance.material", "diffuseColor 0 0 0"); my2Axis->start.setValue(SbVec2f(0.,-6.)); my2Axis->end.setValue(SbVec2f(4.*PI,6.)); my2Axis->xTitle = "Multiple curves"; // Create the root of the scene graph SoSeparator *root = new SoSeparator; root->ref(); #ifdef USE_PB // Define domain PbDomain myDom(0.,-6.,4.*PI,6.); myCurve1->setDomain(&myDom); myCurve2->setDomain(&myDom); my2Axis->setDomain(&myDom); #else PoDomain *myDom = new PoDomain; myDom->min = SbVec3f(0,-6,0); myDom->max = SbVec3f(4.*PI,6.,0); root->addChild(myDom); #endif root->addChild(myCurve1); root->addChild(myCurve2); root->addChild(my2Axis); SoXtPlaneViewer *viewer = new SoXtPlaneViewer(myWindow); viewer->setSceneGraph(root); viewer->setBackgroundColor(SbColor(1., 1., 1.)); ...
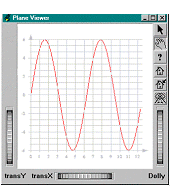
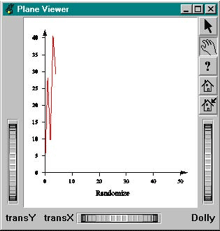
You may want to display real-time data and then animate your curve. The following example (located in $OIVHOME/src/MeshViz/Mentor) shows this capability using an SoTimerSensor( C++ | Java | .NET )sensor from Open Inventor. At each time interval, a random number is generated and added to the curve. The X axis shows the step number and the Y axis the random value. The animation cycles through a maximum number of steps, N_PT. You will notice that the domain changes (no matter what kind of property classes are used) and then the display is updated automatically.
Example 2.19. An animated curve
 |
 |
 |
 |
C++
// tutorialGraph06.cxx ... #define N_PT 50 #define max(a,b) (((a)>(b))?(a)/(b)) // Create the root of the scene graph SoSeparator *root = new SoSeparator; root->ref(); // Create the curve myCurve = new PoCurve; myCurve->point.setValues(0,0,points); myCurve->setDomain(&myDom); myCurve->set("curvePointApp.material", "diffuseColor 1 0 0"); root->addChild(myCurve); // Create a group of 2 axis my2Axis = new PoGroup2Axis; my2Axis->xTitle = "Randomize"; my2Axis->set("appearance.material", "diffuseColor 0 0 0"); my2Axis->setDomain(&myDom); root->addChild(my2Axis); mySensor = new SoTimerSensor(newPointCB, NULL); mySensor->setInterval(10.0); mySensor->schedule(); ... } static void newPointCB(void *, SoSensor *) { int i; float newy,ymax,x,y; newy = 50. * rand()/RAND_MAX; points[cur_n_pt].setValue(cur_n_pt,newy); if(cur_n_pt < N_PT - 1) cur_n_pt++; else { cur_n_pt=0; myCurve->point.setNum(0); return; } ymax = newy; for (i=0; i < cur_n_pt; i++) { points[i].getValue(x,y); ymax = max(ymax, y); } myDom.setDomain(0,0,N_PT,ymax); my2Axis->end.setValue(SbVec2f(N_PT,ymax)); myCurve->point.setValues(0,cur_n_pt,points); mySensor->schedule(); }
The purpose of this section is to show the use of domain functionality when you want to draw multiple data sets which share the same X axis but have different Y domains. In the following example we are going to mix a bar chart representation with a curve representation. Each of the representations has a different Y domain but shares the same X domain.
Two things may be tricky when mixing axes like this. First, you must compute the Y translation for the second axis so that its origin will line up with the origin of the first Y axis. Then you must compute the X translation for the second Y axis so that it does not overlap the first one.
To compute the first translation, you must remember the domain transformation. Then you must compute the scale and/or the translation applied to the Y-axis coordinates because of this transformation. In our example we use the SCALE_X_FIXED transformation. This means that X will not be scaled and Y will be scaled by dx/dy (refer to the domain section in the Section 2.1, “ What You Must Know about MeshViz XLM: ”). Our first axis domain is from -1 to 1 in Y and from 0 to 13 in X. All Y coordinates are thus scaled using a 2/13 factor. So the curve’s Y axis origin is (-1. * 13. / 2.) after the domain transformation. We can apply the same method to the bar chart’s Y axis. Its domain is from -10 to 20 for Y and from 0 to 13 for X. So the transformed Y origin is (-10. * 13. / 30.). We now have both Y coordinates in the same space where we will compute the translation to be applied. To compute the second translation, we will use the SoGetBoundingBoxAction( C++ | Java | .NET )action from Open Inventor. This action, when applied to the root of an axis system, will give you the real bounding box of this system, including ticks, arrows, and text strings. We can use the following skeleton if we want to build a visualization with multiple curves:
For all axis systems:
This method allows you to build as many non-overlapping Y axes as you want. You can also, of course, use the same method if you want to have multiple X axes or multiple axes wherever you want. In fact, you can use the translation value to add a translation node to your scene graph or use this value as the X axis origin of your new axis (the next example, located in $OIVHOME/src/MeshViz/Mentor, uses this second solution).
Example 2.20. A curve and a histogram sharing two different Y axes but the same X axis
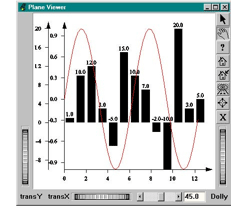
C++
// tutorialGraph07.cxx ... #define N_PT 50 #define PI 3.1315 // Create the curve PoCurve *myCurve = new PoCurve; SbVec2f points[N_PT]; double ang; int i; for (i=0, ang=0.; i < N_PT; i++, ang += 4.*PI/(double)N_PT) points[i].setValue(ang, sin(ang)); myCurve->point.setValues(0,N_PT,points); myCurve->set("curvePointApp.material", "diffuseColor [1 0 0]"); // Create the root of the scene graph SoSeparator *root = new SoSeparator; root->ref(); // Domain of the curve #ifdef USE_PB PbDomain myCurveDom(0.,-1.,13.,1.); myXAxis->setDomain(&myCurveDom); myCurveYAxis->setDomain(&myCurveDom); myCurve->setDomain(&myCurveDom); #else PoDomain *myCurveDom = new PoDomain; myCurveDom->min = SbVec3f(0,-1,0); myCurveDom->max = SbVec3f(13,1,0); root->addChild(myCurveDom); #endif root->addChild(myXAxis); root->addChild(myCurveYAxis); root->addChild(myCurve); // We compute the bounding box of the first axis system // So we will know how to translate the second Y axis SoGetBoundingBoxAction myAction(SbViewportRegion(1000,1000)); myAction.apply(root); float xmin,ymin,zmin,xmax,ymax,zmax; myAction.getBoundingBox().getBounds(xmin,ymin,zmin,xmax,ymax,zmax); // Create the bar chart PoSingleHistogram *myHist = new PoSingleHistogram; myHist->start.setValue(0.,0.); myHist->end = 13.; float values[13] = {1.,10.,12.,3.,-5.,15.,10.,7.,-2.,-10.,20.,3.,5.}; myHist->value.setValues(0,13,values); myHist->set("appearance.material", "diffuseColor 0 0 0"); // Create Y axis for the bar chart PoLinearAxis *myHistYAxis = new PoLinearAxis; myHistYAxis->start.setValue(SbVec3f(xmin,-10.,0.)); myHistYAxis->set("appearance.material", "diffuseColor 0 0 0"); myHistYAxis->end = 20.; myHistYAxis->type = PoCartesianAxis::YX; // Domain of the histogram #ifdef USE_PB PbDomain myHistDom(0.,-10,13.,20.); myHistYAxis->setDomain(&myHistDom); myHist->setDomain(&myHistDom); #else PoDomain *myHistDom = new PoDomain; myHistDom->min = SbVec3f(0,-10,0); myHistDom->max = SbVec3f(13,20,0); root->addChild(myHistDom); #endif // Now we have to align horizontally the two Y axis SoTranslation *myTrans = new SoTranslation; float trans; trans = (-130./30.) - (-13./2.); myTrans->translation.setValue(0.,-trans,0.); // Complete the scene graph (The curve will be drawn after bar chart. // The translation should only apply to the bar chart and its Y axis root->addChild(myTrans); root->addChild(myHistYAxis); root->addChild(myHist); SoXtPlaneViewer *viewer = new SoXtPlaneViewer(myWindow); viewer->setSceneGraph(root); viewer->setBackgroundColor(SbColor(1., 1., 1.)); ...
If you draw business graphs you may want to identify the different parts of your visualization. In this section we are going to look at the PoItemLegend( C++ | Java | .NET )node derived from PoLegend( C++ | Java | .NET )class. All key nodes derived from this class will be illustrated in the 3DdataMaster part of this manual. When you draw curves with GraphMaster, you may use a line representation or draw it using markers for instance. The PoItemLegend( C++ | Java | .NET ) node allows you to annotate your visualization with legends corresponding to the different types of visualization you use in your display. Items in the legend include an optional text string, an optional colored box, an optional set of markers, and an optional line. You can change the appearance of each of these parts. The items may be arranged in one or several columns. Depending on the size of the bounding box of all items (which you specify when you create the legend node), GraphMaster will compute the text height, the box sizes, the number of markers to be drawn, and/or the length of the lines. You cannot control these attributes, but you can adjust margins around these items and the aspect ratio of the filled boxes. Here are some examples of legends you can create:
 |
 |
 |
The following example (located in $OIVHOME/src/MeshViz/Mentor) draws a set of curves and then adds a legend to the display in order to identify these curves.
Example 2.21. Adding a legend to your set of curves
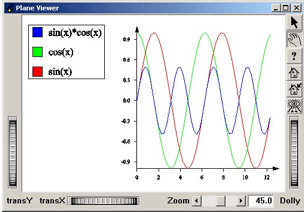
C++
// tutorialGraph08.cxx
...
// Create the legend
PoItemLegend *myLegend = new PoItemLegend;
myLegend->start.setValue(-10.,7.);
myLegend->end.setValue(-3,2);
myLegend->item.set1Value(0,"sin(x)");
myLegend->item.set1Value(1,"cos(x)");
myLegend->item.set1Value(2,"sin(x)*cos(x)");
SbColor colors[3] =
{
SbColor(1., 0., 0.),
SbColor(0., 1., 0.),
SbColor(0., 0., 1.)
};
myLegend->boxColor.setValues(0, 3, colors);
myLegend->set("backgroundApp.material",
"diffuseColor 1 1 1");
myLegend->set("backgroundBorderApp.material",
"diffuseColor 0 0 0");
myLegend->set("boxBorderApp.material",
"diffuseColor 0 0 0");
myLegend->set("valueTextApp.material",
"diffuseColor 0 0 0");
#define PI 3.1415
#define N_PT 50
// Create X axis
PoLinearAxis *myXAxis = new PoLinearAxis;
myXAxis->set("appearance.material",
"diffuseColor 0 0 0");
myXAxis->start.setValue(SbVec3f(0.,-1.,0.));
myXAxis->end = 4.*PI;
myXAxis->type = PoCartesianAxis::XY;
// Create Y axis
PoLinearAxis *myYAxis = new PoLinearAxis;
myYAxis->set("appearance.material",
"diffuseColor 0 0 0");
myYAxis->start.setValue(SbVec3f(0.,-1.,0.));
myYAxis->end = 1.;
myYAxis->type = PoCartesianAxis::YX;
// Create the curves
double ang;
int i;
PoCurve *myCurve1 = new PoCurve;
SbVec2f points1[N_PT];
for (i=0, ang=0.; i < N_PT; i++, ang += 4.*PI/(double)N_PT)
points1[i].setValue(ang, sin(ang));
myCurve1->point.setValues(0,N_PT,points1);
myCurve1->set("curvePointApp.material",
"diffuseColor [1 0 0]");
PoCurve *myCurve2 = new PoCurve;
SbVec2f points2[N_PT];
for (i=0, ang=0.; i < N_PT; i++, ang += 4.*PI/(double)N_PT)
points2[i].setValue(ang, cos(ang));
myCurve2->point.setValues(0,N_PT,points2);
myCurve2->set("curvePointApp.material",
"diffuseColor [0 1 0]");
PoCurve *myCurve3 = new PoCurve;
SbVec2f points3[N_PT];
for (i=0, ang=0.; i < N_PT; i++, ang += 4.*PI/(double)N_PT)
points3[i].setValue(ang, sin(ang) * cos(ang));
myCurve3->point.setValues(0,N_PT,points3);
myCurve3->set("curvePointApp.material",
"diffuseColor [0 0 1]");
// Create the root of the scene graph
SoAnnotation *root = new SoAnnotation;
root->ref();
root->addChild(myLegend);
#ifdef USE_PB
// Define domain
PbDomain myDom(0.,-1.,4.*PI,1.);
myXAxis->setDomain(&myDom);
myYAxis->setDomain(&myDom);
myCurve1->setDomain(&myDom);
myCurve2->setDomain(&myDom);
myCurve3->setDomain(&myDom);
#else
PoDomain *myDom = new PoDomain;
myDom->min = SbVec3f(0,-1,0);
myDom->max = SbVec3f(4.*PI,1.,0);
root->addChild(myDom);
#endif
root->addChild(myXAxis);
root->addChild(myYAxis);
root->addChild(myCurve1);
root->addChild(myCurve2);
root->addChild(myCurve3);
SoXtPlaneViewer *viewer = new SoXtPlaneViewer(myWindow);
viewer->setSceneGraph(root);
viewer->setBackgroundColor(SbColor(1., 1., 1.));
...
You may have noticed in the previous example that the legend is transformed in the same way as the curves during camera manipulation. If the plane viewer is replaced by an Examiner Viewer and if we change the 3D view, we will then get a display like this.

Since we did not define any camera in the previous examples, the plane or examiner viewers add their own at the top of our scene graph to manipulate the scene.
![[Tip]](../../images/tip.jpg) | |
To avoid any view transformation inheritance in the legend node, all we have to do is add our own camera node to the scene graph, between the legend node and the axis and curves nodes. The viewers will then use this camera and any changes made to this camera will affect the axes and the curves, but not our legend node. In the following code, you will notice the changes for the start and end fields of the legend node. As the legend will not be affected by the viewer camera nor by the camera we have included in the scene graph, the default view will be used to render this node, and the default space for this view is [-1,1]x[-1,1]. |
![[Note]](../../images/note.jpg) | |
Furthermore, MeshViz supplies classes to manage multiple views. These classes are PoBaseView( C++ | Java | .NET ) ,PoView( C++ | Java | .NET ) , and PoSceneView( C++ | Java | .NET ) (see the Reference Manual for more information). |
Example 2.22. Adding a legend that is independent of the viewing
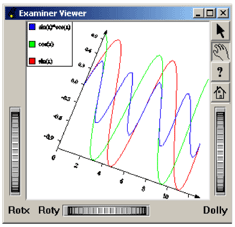
C++
... // Create the legend PoItemLegend *myLegend = new PoItemLegend; myLegend->start.setValue(-1.,1.); myLegend->end.setValue(-.5,.5); myLegend->item.set1Value(0,"sin(x)"); ... root->addChild(myLegend); SoPerspectiveCamera *myCamera = new SoPerspectiveCamera; root->addChild(myCamera); // Define domain of curve and its axis. #define PI 3.1415 PbDomain myDom(0.,-1.,4.*PI,1.); ... SoXtExaminerViewer *viewer = new SoXtExaminerViewer(myWindow); myCamera->viewAll(root, viewer->getViewportRegion()); viewer->setSceneGraph(root); ...

All that we have seen concerning 2D applies in the same way to 3D. Instead of a 2D domain, we will deal with a 3D domain. The following example (located in $OIVHOME/src/MeshViz/Mentor) builds a 3D curve and displays it with its 3D axis system. Here we will use the PoGroup6Axisnode. As with PoGroup2Axis( C++ | Java | .NET )which we have already used, the SO_GET_PART Open Inventor macro may be used to retrieve each axis of the node kit. You can then customize each axis if the default representation does not suit your needs.
Example 2.23. Representing a 3D curve
C++
// tutorialGraph09.cxx ... #define N_PT 50 #define PI 3.1415 // Create the curve double ang, radius; int i; PoCurve3 *myCurve = new PoCurve3; SbVec3f points[N_PT]; ang = 0; radius = 0.; for (i=0; i < N_PT; i++, ang += 6.*PI/(double)N_PT, radius += 10./(double)N_PT) points[i].setValue(radius * cos(ang), radius * sin(ang), 2. *radius); myCurve->point.setValues(0,N_PT,points); myCurve->set("curvePointApp.material", "diffuseColor [1 0 0]"); myCurve->set("curvePointApp.drawStyle", "linewidth 3."); // Create the group of axis PoGroup6Axis3 *my6Axis = new PoGroup6Axis3; my6Axis->set("appearance.material", "diffuseColor 0 0 0"); my6Axis->start.setValue(-10.,-10.,0.); my6Axis->end.setValue(10.,10.,20.); // Create the root of the scene graph SoSeparator *root = new SoSeparator; root->ref(); // Define domain of curve and its axis. #ifdef USE_PB PbDomain myDom(-10.,-10.,0.,10.,10.,20.); myCurve->setDomain(&myDom); my6Axis->setDomain(&myDom); #else PoDomain *myDom = new PoDomain; myDom->min = SbVec3f(-10.,-10.,0.); myDom->max = SbVec3f(10.,10.,20.); root->addChild(myDom); #endif root->addChild(myCurve); root->addChild(my6Axis); SoXtExaminerViewer *viewer = new SoXtExaminerViewer(myWindow); viewer->setSceneGraph(root); viewer->setBackgroundColor(SbColor(1., 1., 1.)); ...
GraphMaster supplies a package of more than fifty classes specifically targeting high level 3D business visualization. Easy to use, this package brings the power of 3D graphics to your business data. These representations include: high level display of curves as tubes, ribbons or “wall curves” with variable thickness and material mapping; customized 3D histograms; 3D pie charts with beveled edges; and an amazing variety of other chart types.
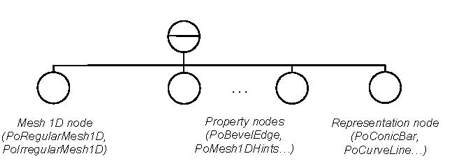
GraphMaster has three categories of nodes:
Data storage nodes: These are one-dimensional meshes (meshes inherited from the abstract class PbMesh1D( C++ | Java | .NET ) ) used for charting representations. Data storage is independent of the 3D representation.
Property nodes: These nodes allow the user to specify the appearance of the representations nodes.
Representation nodes: These are node kits, all inherited from PoChart( C++ | Java | .NET ) , to draw tubes, ribbons,…
A classical scene graph using these nodes looks like the following:
The mesh classes usually used for 3DdataMaster representations have been extended to one-dimensional meshes in order to store data for charting representations.
![[Important]](../../images/important.jpg) | |
The PoIrregularMesh1D( C++ | Java | .NET ) and PoRegularMesh1D( C++ | Java | .NET ) nodes derived from the class PoMeshProperty( C++ | Java | .NET ), respectively contain the fields PoSFIrregularMesh1D( C++ | Java | .NET ) and PoSFRegularMesh1D( C++ | Java | .NET ) , themselves containing an instance derived from PbMesh1D( C++ | Java | .NET ) . |
Property nodes specify the appearance of the representation classes. Only classes inherited from PoChart( C++ | Java | .NET ) take into account these properties.
This node defines the current values to bevel edges of all subsequent MeshViz representations inheriting from PoChart( C++ | Java | .NET ). Some representations, such as pie charts, take into account these attributes to chamfer specific edges.
PoMesh1DFilter( C++ | Java | .NET )
Filter nodes allow the geometry of the current 1D mesh (PoIrregularMesh1D or PoRegularMesh1D( C++ | Java | .NET )) to be filtered. Filtering consists of selecting particular points from the 1D mesh geometry. Only these points are used by subsequent representations inheriting from PoChart( C++ | Java | .NET )in a scene graph.
This node specifies the current period index filter for subsequent MeshViz representations inheriting from PoChart( C++ | Java | .NET ). One point every index period is selected from the geometry of the current 1D mesh by all subsequent representations.
This node specifies the current index list filter for subsequent MeshViz representations inheriting from PoChart( C++ | Java | .NET ). A list of points is selected by their indices from the geometry of the current 1D mesh by all subsequent representations.
This node specifies the current period filter for subsequent MeshViz representations inheriting from PoChart( C++ | Java | .NET ). One point every period is selected from the geometry of the current 1D mesh.
This node specifies the current coordinate list filter for subsequent MeshViz representations inheriting from PoChart( C++ | Java | .NET ). A list of points is selected by their coordinates from the geometry of the current 1D mesh.
This node specifies the current hints for the current 1D mesh. All subsequent representations inheriting from PoChart( C++ | Java | .NET )use these hints for their computation.
PoProfile( C++ | Java | .NET )
A profile specifies a 2D polygon which is used by some charting representations to build their geometry. For instance, for the tube curve representation PoTube( C++ | Java | .NET ), the current profile is used to determine the profile of the tube.
Defines the current hints for the display of labels for subsequent MeshViz representations inheriting from PoChart( C++ | Java | .NET ).
Figure 2.46. Property node classes for charting
The following visualization nodes may apply to 1D meshes:
PoGraphMaster( C++ | Java | .NET )
Abstract base class for all charting representations.
The field PoChart::yValuesIndexspecifies the index of the set of values of the current 1D mesh used as the y-coordinates of each mesh node.
The field PoChart::colorBindingspecifies how the colors are bound to the representation:
INHERITED: The entire representation is colored with the same inherited color.
PER_VERTEX: Each vertex of the representation is colored with a different color from the field PoChart::material or PoChart::colorValuesIndex.
PER_PART: Each part of the representation is colored with a different color from the field PoChart::material or PoChart::colorValuesIndex.
PoCurveLine( C++ | Java | .NET )
To build a 2D curve line. The thickness of the curve can be constant or may depend on a value-set of the current 1D mesh.
A generalized scatter representation is a marker field representation where each marker is defined by a scene graph.
A scatter representation is a bitmap marker field (the SoMarkerSet( C++ | Java | .NET )shape is used for this representation).
To build a 3D pie chart. The height of each slice can be constant or may depend on the value-set of the current 1D mesh.
To draw a label field.
Figure 2.47. Enhanced business graphics node classes
The following example (located in $OIVHOME/src/MeshViz/Mentor) displays a tube curve with an elliptic profile curve where the thickness and the color is variable for each vertex of the curve.
Example 2.24. A tube curve
C++
// tutorialGraph10.cxx ... #define NP 14 float x[NP] = { 0.5, 1.5, 1.8, 2.4, 3.2, 4.5, 6.3, 6.9, 8.0, 8.5, 9.0, 9.5, 9.8, 10 }; float y[NP] = { 9.0, 7.0, 6.5, 6.0, 5.0, 5.5, 6.0, 7.7, 6.8, 6.0, 5.5, 4.5, 3.5, 2.5 }; float size[NP] = {1, 3, 5, 1, 3, 5, 1, 3, 5, 1, 3, 5, 1, 3}; SbColor colorListD[3] = { SbColor(1,0,0), SbColor(0, 1, 0), SbColor(0, 0, 1) }; // Domain of the representation from [0,0,-1] to [10,1O,1] PoDomain *myDomain = new PoDomain; myDomain->min.setValue(0., 0., -1); myDomain->max.setValue(10., 10., 1); // Font use for axis PoMiscTextAttr *myTextAttr = new PoMiscTextAttr; myTextAttr->fontName = "Courier"; SoSeparator *root = new SoSeparator; // Define the irregular 1D mesh for the geometry of the tube curve. PoIrregularMesh1D *mesh1D = new PoIrregularMesh1D; mesh1D->setGeometry(NP, x); // Abscissas of the tube. mesh1D->addValuesSet(0, y); // Ordinates of the tube. mesh1D->addValuesSet(1, size); // Values-set for the variable // sizes of the tube. // The tube will be smoothed. PoMesh1DHints *mesh1DHints = new PoMesh1DHints; mesh1DHints->geomInterpretation = PoMesh1DHints::SMOOTH; // Material use by the tube. SoMaterial *mat = new SoMaterial; mat->diffuseColor.setValues(0, 3, colorListD); // Defined the elliptic profile of the tube. PoEllipticProfile *profile = new PoEllipticProfile; profile->xRadius = 0.15; profile->yRadius = 0.025; // Define the tube curve representation. PoTube *tube = new PoTube; tube->material.setValue(mat); tube->colorBinding = PoTube::PER_VERTEX; tube->thicknessFactor = 0.5; tube->thicknessIndex = 1; // Defines the three axis. PoGroup2Axis *g2Axis = new PoGroup2Axis(SbVec2f(0.,0.), SbVec2f(10., 10.), PoGroup2Axis::LINEAR, PoGroup2Axis::LINEAR, "X-Axis", "Y-Axis"); PoLinearAxis *zAxis = new PoLinearAxis(SbVec3f(0,0,-1), 1, PoLinearAxis::ZY); // Builds the scene graph. root->ref(); root->addChild(mesh1D); root->addChild(myDomain); root->addChild(myTextAttr); root->addChild(mesh1DHints); root->addChild(profile); root->addChild(tube); root->addChild(zAxis); root->addChild(g2Axis); // Builds the examiner viewer. SoXtExaminerViewer *viewer = new SoXtExaminerViewer(myWindow); viewer->setSceneGraph(root); viewer->setTitle("Tube"); ...
The size of the text on your axis is expressed as a percentage of the domain. This is also true for certain other axis attributes and other representations. Either you have forgotten to define a domain (PoDomain), or you have not defined it correctly.
There are several reasons for the existence of the domain.
First imagine that you have a curve that ranges from 0 to 1 along the x-axis and from 0 to 1000 in the y-axis. You want to represent this curve and also the axis system associated with it.
If you don’t use a transformation, the resulting display will not be legible because the y-axis is very large compared to the x-axis. Intuitively you will want to scale the y-axis relative to the x-axis (or vice versa) in order to obtain something legible. If you do this using an SoScale( C++ | Java | .NET ), it will work for the curve representation (PoCurve) but you will have some problems with the axis representation (PoLinearAxis). Specifically, you will note that the graduation labels as well as the arrow at the end of the axis will appear very flattened along the direction of the Y-axis. So, applying a simple scale transformation is not the correct way to achieve a good result because some parts of your representation need to be uniformly scaled but not others.
The property node PoDomain( C++ | Java | .NET ) addresses these kinds of problems.
Second, many fields of MeshViz nodekits are expressed in the space defined by the current domain. The chapter on Domains of the MeshViz User’s Guide provides additional details about the use of domains.
Generally, you define the domain values as the bounding box of your data and you obtain a square representation.
For instance, if you want to have an X-axis from 0 to 1 and a Y-axis from 0 to 10, you set the domain (PoDomain) fields to: min (0,0,0) and max (1,10,1).
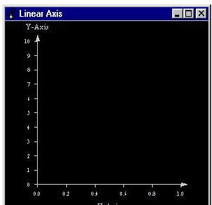
Now, if you want to obtain an X-axis which is double the size of the Y-axis, you must define a domain which has double the size of the Y-data -- that is, min (0,0,0) and max (1,20,1) -- and you obtain the following:
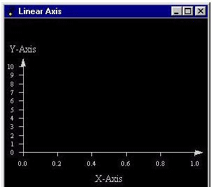
In the first case (square representation), the scale applied by the PoDomain( C++ | Java | .NET ) to the axis is the following:
min and max are the fields of the PoDomain( C++ | Java | .NET ) node.
dx = max[0] - min[0]
dy = max[1] - min[1]
dz = max[2] - min[2]
Sx = 1: the end coordinate of the X-Axis is 1.
Sy = dx/dy = 1 / 10 = 0.1 -> the top coordinate of the Y-Axis is 10 x 0.1 = 1.
Sz = dx/dz = 1 / 1 = 1
In the second case (rectangular representation), the scale applied by the PoDomain( C++ | Java | .NET ) to the axis is the following:
Sx = 1 : the end coordinate of the X-Axis is 1.
Sy = dx/dy = 1 / 20 = 0.05 -> the top coordinate of the Y-Axis is 10 x 0.05 = 0.5
Sz = dx/dz = 1 / 1 = 1
As described in the previous question, defining the domain values as the bounding box of your data gives a square representation. However if you absolutely need to preserve the aspect ratio of your data, you can use the PoDomain( C++ | Java | .NET )::setValues() method with the last argument set to MIN_BOUNDING_CUBE.
For instance, if you want to have an X-axis from 0 to 1 and an Y-axis from 0 to 5, and preserve the original (1 to 5) aspect ratio:
myDomain->setValues(SbVec3f(0,0,0), SbVec3f( C++ | Java )(1,5,1), PoDomain( C++ | Java | .NET )::MIN_BOUNDING_CUBE);

All MeshViz shapes automatically insert in their catalog kit (part named domainTransform) a transformation which corresponds to the domain, so these shapes are automatically transformed. For Open Inventor shapes, you must add this transformation to the scene graph manually just before the shape to be transformed. To get the transformation that should be applied, call the PoDomain( C++ | Java | .NET )::getMatrixTransform() method which returns an SoMatrixTransform( C++ | Java | .NET ).
All MeshViz representations ignore the node SoFont( C++ | Java | .NET ) for selecting the font name and size. Instead the property node PoMiscTextAttr( C++ | Java | .NET ) is used for this purpose.