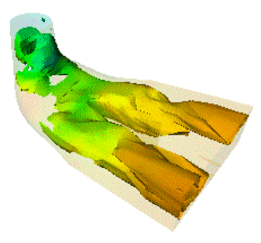
3DdataMaster defines extension nodes to Open Inventor primarily for the development of scientific visualizations. Before going any further it is very important to have read Section 2.1, “ What You Must Know about MeshViz XLM: ”.
Important note:
The C++ implementation of 3DdataMaster is kept for compatibility with older versions. You should use MeshViz Interface instead of 3DdataMaster.
For Java and .NET developers, since implementing C++ interfaces in other languages is not possible without writing heavy cross language bridges, we recommand to continue to use 3DdataMaster.
All mesh types are derived from the PbMesh( C++ | Java | .NET )basic type. A mesh definition is basically given by a set of value sets. The following methods are used to initialize the meshes. The addValuesSet()method allows you to add a set of values to your mesh; removeValuesSet()or removeAllValuesSet()allows you to remove one or all of the sets. The getNumValuesSet()method returns the number of value sets associated with a mesh; getMinValuesSet()and getMaxValuesSet()return the minimum and the maximum values for a given set. For example, a value set may be the list of temperatures for each node of your mesh, or a list of pressures for each cell of your mesh. The setGeometry()method is defined for each of the basic types and allows you to initialize the node coordinates of your mesh. Please refer to PbMesh( C++ | Java | .NET )and its derived classes for a full description of these methods.
To visualize data from a mesh, you must instantiate a class derived from PoMesh( C++ | Java | .NET ) , depending on the type of visualization you need. For example PoMeshSkin( C++ | Java | .NET )allows you to visualize the skin of a volume mesh. These classes are derived from Open Inventor node kits and we call them “visualization node kits.”
As a visualization node kit depends, of course, on the data describing the mesh, you must also define a relationship between the PoMesh( C++ | Java | .NET ) instance and the PbMesh( C++ | Java | .NET )instance. MeshViz provides two ways to specify this relation:
Call PoMesh::setMesh(PbMesh *pb_mesh) for each instance derived from PoMesh( C++ | Java | .NET )that visualizes data from “pb_mesh”. The Open Inventor shapes contained in the visualization node kit are automatically updated whenever necessary or when you force an update by calling PoMesh::rebuild(). See also the connection mechanism described in the section called “ Property and Visualization Classes”.
Create an instance of a derived class of PoMeshProperty( C++ | Java | .NET ) , which is an Open Inventor node containing an Open Inventor field derived from PoSFMesh( C++ | Java | .NET ) , itself containing an instance derived from PbMesh( C++ | Java | .NET ) . Then you must add this property mesh node to the scene graph so that it will be inherited during traversal and used by the different visualization node kits you define. The methods setGeometry()and addValuesSet()are also available in the subclasses of PoMeshProperty( C++ | Java | .NET )class and build for you the instance of the contained PbMesh( C++ | Java | .NET )object.
![[Note]](../../images/note.jpg)
See also the the section called “ Property and Visualization Classes”.
The PoMesh::coloringTypefield of the visualization node allows you to select the type of coloring that will be applied if necessary (refer to the following the section called “ Surface Meshes”, for the explanation of these coloring methods). If data mapping coloringTypeis not COLOR_INHERITED, a data mapping object must be created to specify the data-to-color mapping, and if coloringTypeequals COLOR_CONTOURING or COLOR_TEXTURE_CONTOURING, an isovalueList object must be created to specify the list of isovalues. A data mapping object is defined by an instance of either the class PbDataMapping( C++ | Java | .NET )or the class PoDataMapping( C++ | Java | .NET ). An isovalueList object is defined by an instance either of the class PbIsovaluesList( C++ | Java | .NET )or the class PoIsovaluesList( C++ | Java | .NET ). (Refer to the section called “ Data-to-Color Mapping” and the section called “ Defining Isovalues”).
![[Important]](../../images/important.jpg) | |
When coloring a value set that has its values located at a cell (see the section called “Location of values”), the cells are always colored with a unique color even when the color type (coloringType field) is COLOR_AVERAGE, COLOR_MAPPING, COLOR_CONTOURING, or COLOR_TEXTURE_CONTOURING. |
The following code fragments define the objects necessary to visualize the skin and a cross-section of a volume mesh. This example uses the Pbxxxobjects and the PoMesh::setxxx(Pbxxx*pb) methods.
Example 2.25. Visualize a skin and a cross-section of a volume mesh
C++
PbCartesianGrid3D pb_mesh; pb_mesh.setGeometry(...); pb_mesh.addValuesSet(data_index,dataset); PbLinearDataMapping pb_datamapping; PoMeshSkin *skin = new PoMeshSkin; skin->coloringType = PoMesh::COLOR_MAPPING; skin->valuesIndex(data_index); skin->setMesh(&pb_mesh); skin->setDataMapping(&pb_datamapping); PoMeshCrossSection *cross_section = PoMeshCrossSection; cross_section->coloringType = PoMesh::COLOR_MAPPING; cross_section->valuesIndex(data_index); cross_section->setMesh(&pb_mesh); cross_section->setDataMapping(&pb_datamapping); SoGroup *group = new SoGroup; group->addChild(skin); group->addChild(cross_section);
Example 2.26. Uses the Po property nodes included in the scene graph
C++
PoCartesianGrid3D *po_mesh = new PoCartesianGrid3D;
po_mesh->setGeometry(...);
po_mesh.addValuesSet(data_index,dataset);
PoLinearDataMapping *po_datamapping =
new PoLinearDataMapping;
PoMeshSkin *skin = new PoMeshSkin;
skin->coloringType = PoMesh::COLOR_MAPPING;
skin->valuesIndex(data_index);
PoMeshCrossSection *cross_section = PoMeshCrossSection;
cross_section->coloringType = PoMesh::COLOR_MAPPING;
cross_section->valuesIndex(data_index);
SoGroup *group = new SoGroup; group->addChild(po_mesh);
group->addChild(po_datamapping);
group->addChild(skin);
group->addChild(cross_section);
The values of a mesh can be located either at the cells of the mesh or at the nodes of the mesh.
When the values are located at a cell, each cell is drawn with only one color. For instance when drawing a cross-section, the shape used to draw the intersection between the plane and a cell is colored with one color. When drawing the skin of a mesh, the face of a cell that “belongs” to the skin is also colored with one color. The color used depends on the value of this cell.
![[Warning]](../../images/warning.jpg) | |
At this time, value sets with per-cell data can only be used by the classes PoMeshLevelSurf( C++ | Java | .NET ), PoMeshSkin( C++ | Java | .NET ), and PoMeshCrossSection( C++ | Java | .NET ). |
To define a value set with values located at the cells of the mesh, use the following method:
C++
my_mesh->addValuesSet(set_index, cell_values, PER_CELL);
When the values are located at the nodes of the mesh, each cell is drawn using the values of each node of the cell. How these nodes’ values are used to draw the cell depends on the coloring mode. (see the section called “Mesh coloring”).
To define a values set located at node, use the following method:
C++
my_mesh->addValuesSet(set_index, cell_values, PER_NODE);
Filtering cells is a way to specify which cells are used to build the mesh representation. A cell filter is based only on the method acceptCell() of the class PoCellFilter( C++ | Java | .NET ) . When acceptCell() returns TRUE, the cell given as the argument is used for the representation, otherwise the cell is not taken into account by the representation.
A cell filter does not apply any transparency to a rejected cell. When a cell is not accepted, it is as if the mesh did not contain this cell. A transparency applied to a cell of mesh skin would create a hole in the surface, whereas the cell filter actually modifies the geometry of the skin.
In order to define a custom cell filter, you must create a class derived from PoCellFilter( C++ | Java | .NET ) and implement the method acceptCell() per your needs. It has two arguments, the index of the cell, and the float value at this cell. This allows you to filter the cell based on its index or a property at this cell. For instance, a filter could eliminate all cells having a value greater than a specified value, or eliminate the last 100 cells of the mesh.
The value passed as the second argument to acceptCell() is an element of the scalar data set currently selected by the representation. This data set is selected by setting the field PoMesh::valuesIndexForCellFilter .
The class PoIntervalCellFilter( C++ | Java | .NET )is a predefined implementation of a cell filter. It implements the acceptCell() method by simply checking if the value of a cell is between a given min and max range.
Example 2.27. Visualize a skin using a cell filter based on the float value at the cell
The filter rejects each cell whose value (here property_for_filter) is not between 100 and 200.
C++
float property_for_color[NUM_NODES]; float property_for_filter[NUM_CELLS]; PoHexahedronMesh3D mesh; mesh.setGeometry(...); mesh.addValuesSet(0, property_for_color); // gives a property that is used to // compute the colors of the skin mesh.addValuesSet(1, property_for_filter, PbMesh::PER_CELL); // gives a property for //each cell, that will be used by the filter PoMeshSkin *skin = new PoMeshSkin; skin->coloringType = PoMesh::COLOR_MAPPING; skin->valuesIndex(0); skin->valuesIndexForCellFilter (1); // select the property_for_filter as the data // set used by the filter PoIntervalCellFilter * filter = new PoIntervalCellFilter; filter->min = 100; filter->max = 200; filter->in = TRUE; root->addChild(mesh); root->addChild(filter); root->addChild(skin);
In this example, the skin building process calls acceptCell() like this:
For each index of cell (cell_index) {
if acceptCell (cell_index, property_for_filter[cell_index]) is true
then include this cell in the skin
}
If valuesIndexForCellFilter is -1 or if there is no data set corresponding to the specified index, acceptCell() is called with 0 as its second argument.
![[Warning]](../../images/warning.jpg) | |
PoMeshSkin( C++ | Java | .NET ), PoMeshCrossSection( C++ | Java | .NET ), PoMeshLevelSurf( C++ | Java | .NET ), PoMeshCrossContour( C++ | Java | .NET ), PoMeshSkeleton( C++ | Java | .NET ), PoMeshProbePoint( C++ | Java | .NET ), PoBaseStreamLine( C++ | Java | .NET ) (and derived classes), as well as PoMesh3DVecCrossSection( C++ | Java | .NET ), use the cell filter (PoCellFilter( C++ | Java | .NET )) inherited from the scene graph. |
3DdataMaster provides the following types to deal with your 2D and 3D surface meshes (the indentation shows class derivations):
PbCartesianGrid2D
See the section called “ Irregular Cartesian grid”
PbRegularCartesianGrid2D
See the section called “ Polygonal mesh”
PbQuadr angleMesh2D
Figure 2.48. 2D mesh classes
With 2D or 3D surface meshes you can choose to have a simple representation with either solid contouring or line contouring (annotated or not). With 2D meshes you can also choose, using the same representation, a 3D visualization by selecting one of your value sets to define an altitude. You can select a scalar data set as an altitude by using the field PoMesh2D::zValuesIndex .
The following visualization nodes may apply to surface meshes (the indentation shows class derivations):
Po3DdataMaster( C++ | Java | .NET )
To draw the border line of the mesh geometry.
To draw the wireframe visualization of the mesh geometry.
To draw solid contouring using current data-color mapping. Coloring may be:
constant:All the mesh cells are filled with a constant color. (Only lighting may affect the constant coloring.)
average:Each mesh cell will be filled with the color corresponding to the average value of nodes of this cell. The “value to color mapping” (see the section called “ Data-to-Color Mapping”) is defined either by the connected PbDataMapping( C++ | Java | .NET )object or by the PoDataMapping( C++ | Java | .NET )object inherited during traversal.
mapping:Each node value of the mesh defines a color and the mesh is thus filled by interpolating these colors (Gouraud shading). This method does not give the exact contouring areas but gives a very good idea of the result relatively quickly. The “value-to-color mapping” (see the section called “ Data-to-Color Mapping”) is defined as for average mode.
contouring:Each mesh cell is exactly sub-divided into isovalued areas, and each of these areas is then filled with the corresponding color. This last method is the most accurate but because it introduces new polygons, it may slow down the visualization. The “isovalues” (see the section called “ Defining Isovalues”) are defined by the connected PbIsovaluesList object or the PoIsovaluesList object inherited during traversal.
Non manifold meshes are not correctly supported with this mode.
texture contouring: Same as contouring but a texture is used for creating the contours. This method dramatically decreases the amount of generated geometry and speeds up the computation time of filled representations relative to the contouring method. This mode should be used for all animations. This method should not be used for wireframe representations because texturing is not active in wireframe mode. Also, you may see some slight differences compared to contouring for meshes with few cells. Furthermore, in contrast with the contouring mode, non manifold meshes are correctly supported.
WARNING: average, mapping, contouring, and texture contouring modes are not yet supported by the representation nodes of surface meshes when using a data set that has PER_CELL data.

Constant
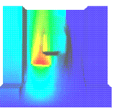
Average
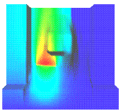
Mapping

Contouring/Texture Contouring
When a 3D visualization is drawn, the vertical faces may be displayed, joining a z = constant plane to the border lines of the mesh.
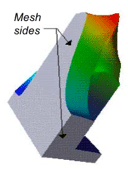
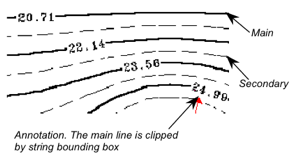
To draw contour lines on your mesh with or without annotations. You can define main and sub lines. Only main lines will be annotated and you can then customize the annotation. For example, if you want them to be included in the contour line with or without a background, you can ask 3DdataMaster to clip the line around the bounding box of the annotation string, you can also force all the annotations to either be horizontal, or vertical or following the line slope, etc. The “contouring-values” (see the section called “ Defining Isovalues”) are defined by the connected PbIsovaluesList( C++ | Java | .NET )object or the PoIsovaluesList( C++ | Java | .NET )object inherited during traversal.
To draw vectors field on a 2D Mesh.
Figure 2.49. Surface mesh representation node classes
3DdataMaster provides the following basic types to deal with your 3D volume meshes (indentation shows class derivation):
Figure 2.50. 3D mesh classes
The following visualization nodes may apply to 3D meshes (indentation shows class derivation):
Po3DdataMaster( C++ | Java | .NET )
PoMeshSkin
To draw the “skin” of the volume mesh, which is the 3D surface separating the exterior from the interior part of the 3D volume defined by the mesh. This skin may be colored using the current data-color mapping method: constant, average, mapping, contouring or texture contouring. Refer to the surface meshes (see the section called “Surface mesh”) section for an explanation of these coloring methods. For indexed volume meshes, this representation also includes the skin of the inside holes.

This class defines a cross-section of the 3D volume and then builds solid contouring visualization on this plane using the current data-color mapping method.

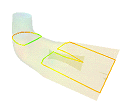
This class builds the intersection between a cross-section of the mesh and its skin. This contour intersection can be colored using the current data-color mapping method. This representation can be useful for visualizing the position of a cross-section. The following image shows a transparent skin and a cross-contour made of two contours.
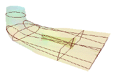
This class draws a 3D skeleton of the 3D mesh by building a set of X, Y and Z plane cross contours. The following image shows a transparent skin and a skeleton made of two X-contours, two Y-contours, and two Z-contours.
This class builds a 3D isosurface. The color of this 3D surface is specified by the current color associated with the surface value. The following image shows a transparent skin and a colored level surface. In this example, two scalar data sets are used to build the level surface. The first one defines the geometry of the level surface and the other one the coloration. The coloration is done using the current “value-to-color mapping” (see the section called “ Data-to-Color Mapping”).

PoMesh3DVec
This class builds a vector field on a volume mesh. Each vector of the vector data set is taken into account to build the representation. The set of vector data is selected by the field PoMesh::vecsIndex.

This class builds a vector field on a cross-section of a volume mesh. A vector is drawn at each of the edges intersecting the cross-section. The value and direction of a vector is computed by linear interpolation between the two nodes of the edge intersecting the cross-section. The set of vector data is selected by the field PoMesh::vecsIndex.
This class builds a vector field on a regular grid mapped onto a cross-section of a volume mesh. The vector at a point P of the grid is interpolated using the vectors at the nodes of the cell that contains P. This class is derived from PoMesh3DVecCrossSection( C++ | Java | .NET ) and may be much more time consuming when choosing a very small grid spacing. For each point of the grid, this class uses a probe tool to find out which cell contains the point. This class behaves like PoMesh3DVecCrossSection( C++ | Java | .NET ) if the grid spacing is null. The following image shows a transparent skin, a cross contour, and a vector field representation mapped onto the same plane as the cross-contour.
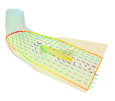
Figure 2.51. Volume mesh representation node classes
The following visualization nodes may apply to surface or volume meshes (indentation shows class derivation):
Po3DdataMaster( C++ | Java | .NET )
PoBaseStreamLine( C++ | Java | .NET )
Abstract class to visualize a vector data set with streamlines, particle motion, or stream-surfaces. The representations can be colored according to a scalar data set, the speed at each point of the line (see the section called “ Data-to-Color Mapping”), or the index of the source (i.e. each line has its own color).
Visualization of streamlines starting from a list of source points. Each streamline is represented by a line. The following image represents a transparent skin and a list of streamlines starting from about 15 sources placed on a circle. The lines are colored according to the velocity.
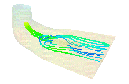
Visualization of a surface that connects several streamlines starting from a list of aligned sources. The following image represents a transparent skin and a stream-surface colored according to the velocity at the points of the surface.

PoStreamParticleMotion( C++ | Java | .NET )
Abstract class that allows animation of particles along a list of streamlines. Of course, the velocity of the particle motion is relative to the velocity on the streamlines. This class allows some control over the animation. For example, you can specify a time step, the number of frames in the animation, etc.
Visualization of animated particles that look like a “tadpole.” Each particle is drawn with a line segment of three points. The length of the segment is proportional to the velocity.

Visualization of animated particles along streamlines. Each streamline is drawn with one color but some points of it are drawn with another color. This other color moves along the streamline, and so does the animation.

Visualization of animated particles. Each particle is represented by a simple point.

Visualization of animated particles. Each particle is represented by a sphere. The animation of these spheres can be slow.
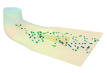
PoCellShape( C++ | Java | .NET )
Abstract class to visualize a cell of a mesh. It can be useful for seeing some details of the geometry of a mesh, especially on a non-structured mesh. The cell to draw is specified by its index in the mesh. Note that the cell to draw can be determined by a callback triggered by the probe class PoMeshProbePoint( C++ | Java | .NET ).
Visualization of the edges of a cell.
Visualization of the facets of a cell. For a surface cell, it only fills the cell; for a volume cell, it fills the skin of the cell.
Visualization of 2D text strings that indicate the index of the cell (drawn at center of the cell) and the indices of each node of the cell (drawn near each node position).
Class that does not draw anything, but triggers four kinds of callbacks depending on changes to its position field. Each callback passes the cell that contains the position as parameter argument. The first callback is triggered each time the probe leaves the mesh (position is out of the mesh, and it was inside before). The second callback is triggered each time the probe enters the mesh (position is inside the mesh and was out before). The third callback is triggered each time the probe moves to a different cell (position was in another cell before). The last callback is triggered each time the position changes. It can be very useful to connect the position field to an Open Inventor dragger.
Figure 2.52. Common mesh representation node classes
MeshViz includes the following property classes which allow you to map a floating value to a color, or to map a set of floating values to a color ramp or several color ramps. Two ways are available to define a data-to-color mapping:
You can instantiate a class derived from PoDataMapping( C++ | Java | .NET )and add this object to the scene graph.
You can instantiate a class derived from PbDataMapping( C++ | Java | .NET ) and call setDataMapping() to connect this data-mapping object to a visualization node. For example, setDataMapping() is available with PoMesh( C++ | Java | .NET ), PoValueLegend( C++ | Java | .NET ), etc.
PoLinearDataMapping or PbLinearDataMapping
Two values, value1 and value2, are associated with color1 and color2, and transparency1 and transparency2, respectively. The color associated with a value between value1 and value2 is a linear interpolation between color1 and color2. In the same way, the associated transparency is a linear interpolation between transparency1 and transparency2. For instance, the following lines define the color-data mapping below:
PoNonLinearDataMapping or PbNonLinearDataMapping
Using the setColorFunction()method, you provide a function that returns an SbColor( C++ | Java ), given a floating value as an input parameter. Each time MeshViz needs to map a floating value to a color, it will call this function. In the same way, the setTransparencyFunction()method provides a function that returns a transparency, given a floating value as an input parameter. Each time MeshViz needs to map a floating value to a transparency, it will call this function.
PoNonLinearDataMapping2 or PbNonLinearDataMapping2
This class defines a set of colors or a set of color ramps associated with floating values. You can choose:
LINEAR_PER_LEVEL type of mapping for a floating value f. If f is in the interval fi, fi+1, its associated color will be the linear interpolation between ci and ci+1 RGB or HLS colors. In this case, you must provide the same number of floating values as the number of colors.
NON_LINEAR_PER_LEVEL type of mapping for a floating value f. If f is in the interval fi, fi+1, its associated color will be the ci+1 th RGB or HLS color; no interpolation is performed. If f is smaller than f1, then c1 is used. In this case, you must provide n+1 colors for n floating values.
Example 2.29. Defining a data mapping with several colors
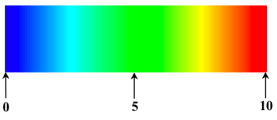
C++float values[5] = {0.0, 2.5, 5., 7.5, 10.}; SbColor colors[5] = { SbColor(0.0,0.0,1.0), SbColor(0.0,1.0,1.0), SbColor(0.0,1.,0.), SbColor(1.0,1.0,0.0), SbColor(1.0,0.0,0.0) }; PoNonLinearDataMapping2 *myDataMapping = new PoNonLinearDataMapping2; myDataMapping->color.setValues(0,5,colors); myDataMapping->value.setValues(0,5,values); myDataMapping->type = PoNonLinearDataMapping2::LINEAR_PER_LEVEL;
The data mapping nodes also allow you to specify threshold values associated with colors. You can specify a minimum threshold or a maximum one using PoDataMapping::minThresholdand PoDataMapping::maxThresholdfields. All values smaller than the minimum threshold are associated with the specified color and, in the same way, values greater than the maximum threshold will be associated with the color of this maximum value.
The threshold effect can be activated and deactivated using the PoDataMapping::maxThresholdEnabledand PoDataMapping::minThresholdEnabledfields.
Sometime it can be useful to visualize meshes that contain some nodes which have a very large or very small value compared to the range of the other nodes’ values. It can be nodes where no calculation, measurement, or probe has been realized. It can be a way to indicate that the scalar value at a node is not assigned, or is not significant for visualization. In the following discussion, we call these special values “undefined values.”
MeshViz provides two ways of handling theses undefined values using the PoDataMapping( C++ | Java | .NET ) nodes (or PbDataMapping( C++ | Java | .NET ) ):
You can visualize the cells, or any shapes that contain at least one undefined value, with a specific color and/or transparency.
You can discard these cells or shapes from the scene graph.
To do that, you must specify in the data-mapping object what are “undefined values.” MeshViz considers any value to be undefined if it is greater than an upper threshold or less than a lower threshold. The upper threshold is set by the field PoDataMapping::maxThresholdand the lower one is set by PoDataMapping::minThreshold . Furthermore, a threshold is activated only if PoDataMapping::maxThresholdEnabledor minThresholdEnabled is TRUE (FALSE by default).
To summarize, a value V is undefined in the following cases:
minThresholdEnabled and maxThresholdEnabled are TRUE, and V is not inside the open interval minThreshold, maxThreshold .
minThresholdEnabled is TRUE, and V is lower than or equal to minThreshold.
maxThresholdEnabled is TRUE, and V is greater than or equal to maxThreshold.
To visualize an undefined value with a specific color, just assign the fields PoDataMapping( C++ | Java | .NET )::maxThresholdColor or PoDataMapping::minThresholdColor .
To visualize an undefined value with a specific transparency, just assign the fields:
PoDataMapping::maxThresholdTransparencyor PoDataMapping::minThresholdTransparency , and assign the field transparencyEnabled to TRUE.
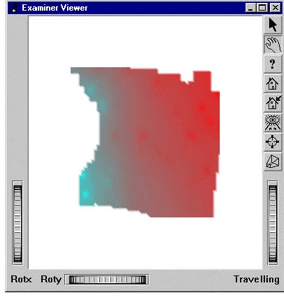
The following example (located in $OIVHOME/src/MeshViz/Mentor) visualizes a rectangular mesh; each cell that contains one or more undefined nodes will be discarded.
Example 2.30. A rectangular mesh with undefined values
C++
// tutorialMesh01.cxx
int
main(int, char **argv)
{
// Initialize Inventor and Xt
Widget myWindow = SoXt::init(argv[0]);
if (myWindow == NULL) exit(1);
// Initialize MeshViz
PoMeshViz::init();
// Read back from file mesh data
// and geometry
int num_x,num_y;
float *xm,*ym, *vm, vmin,vmax,undef;
read_mesh("UNDEFGRID.TOPO", num_x, &xm, num_y, &ym);
read_val("IDESUNI.DAT", num_x*num_y, &vm,vmin,vmax,undef);
// Define data mapping
PoLinearDataMapping *myDataMapping = new PoLinearDataMapping;
myDataMapping->color1 = SbColor(1,0,0);
myDataMapping->value1 = vmin;
myDataMapping->color2 = SbColor(0,1,1);
myDataMapping->value2 = vmax;
myDataMapping->maxThreshold = undef;
myDataMapping->maxThresholdEnabled = TRUE;
myDataMapping->maxThresholdTransparency = 1.0;
myDataMapping->transparencyEnabled = TRUE;
// Initialize the mesh
PoParalCartesianGrid2D *mesh = new PoParalCartesianGrid2D;
mesh->setGeometry(num_x, num_y, xm,ym);
mesh->addValuesSet(0,vm);
// Create the solid contour visualization node.
PoMeshFilled *myFill = new PoMeshFilled;
myFill->valuesIndex.setValue(0);
myFill->coloringType = PoMesh::COLOR_MAPPING;
SoSeparator *root = new SoSeparator;
root->ref();
root->addChild(mesh);
root->addChild(myDataMapping);
root->addChild(myFill);
SoXtExaminerViewer *viewer = new SoXtExaminerViewer(myWindow);
viewer->setSceneGraph(root);
viewer->setBackgroundColor(SbColor(1., 1., 1.));
viewer->show();
SoXt::show(myWindow);
SoXt::mainLoop();
return 0;
}
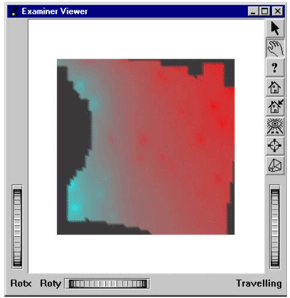
To visualize undefined cells in gray, just replace the two lines:
C++
myDataMapping->maxThresholdTransparency = 1.0;
myDataMapping->transparencyEnabled = TRUE;
by:
C++
myDataMapping->maxThresholdColor =
SbColor(0.2,0.2,0.2);
If you want to do solid or line contouring, you must specify which values you want to display. MeshViz provides the PbIsovaluesList( C++ | Java | .NET ) and PoIsovaluesList( C++ | Java | .NET )classes that allow you to do so. There are two ways to define a list of isovalues:
You can instantiate a class derived from PoIsovaluesList( C++ | Java | .NET )and add this object in the scene graph.
You can instantiate a class derived from PbIsovaluesList( C++ | Java | .NET )and call setIsovaluesList()to connect this object to a visualization node. For example, setIsovaluesList() is available with PoMesh( C++ | Java | .NET ), PoValueLegend( C++ | Java | .NET ), etc.
A list of isovalues can be a list of any floats. However, convenience methods are available to define a regular list. In a regular list, the step size between two consecutive isovalues is a constant. For example, the following methods are available for creating lists:
or:
C++
PoIsovaluesList *myIsoList = new PoIsovaluesList; myIsoList->setRegularIsoList(0.,10.,25);
or:
C++
float values[3] = {0,8,12}; PoIsovaluesList *myIsoList = new PoIsovaluesList; myIsoList->isovaluesList.setValues(0,3,values);
![[Note]](../../images/note.jpg) | |
The isovalue list may be used by the following visualization nodes: |
